Tools

Multipliers

2-Bit Binary Multiplier

Circuit Diagram

2-Bit Multiplier Circuit Diagram

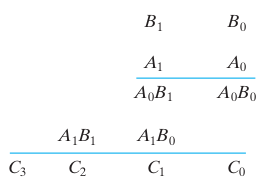
Figure 1: 2-bit multiplier circuit diagram using AND gates for partial product generation and half adders for summation. Reference: Theory section

Components Required

  • 4 AND gates
  • 2 Half adders

Circuit Connections

  1. Drag the first AND gate and connect its inputs to A₀ and B₀. This generates partial product P₀₀.
  2. Drag the second AND gate and connect its inputs to A₀ and B₁. This generates partial product P₀₁.
  3. Drag the third AND gate and connect its inputs to A₁ and B₀. This generates partial product P₁₀.
  4. Drag the fourth AND gate and connect its inputs to A₁ and B₁. This generates partial product P₁₁.
  5. Drag the first Half Adder (HA₁) and connect its inputs to the outputs of the second AND gate (P₀₁) and third AND gate (P₁₀).
  6. Connect the Sum output of HA₁ to output bit C₁.
  7. Drag the second Half Adder (HA₂) and connect its inputs to the Carry output of HA₁ and the output of the fourth AND gate (P₁₁).
  8. Connect the Sum output of HA₂ to output bit C₂.
  9. Connect the Carry output of HA₂ to output bit C₃.
  10. Connect the output of the first AND gate (P₀₀) directly to output bit C₀.
  11. Set the input values for A₁, A₀, B₁, B₀ and click "Simulate".

Observations

  • The output C₃C₂C₁C₀ represents the 4-bit product of the 2-bit multiplicand (A₁A₀) and 2-bit multiplier (B₁B₀).
  • For example: If A₁A₀ = 11₂ (3₁₀) and B₁B₀ = 10₂ (2₁₀), then C₃C₂C₁C₀ = 0110₂ (6₁₀).
  • If the circuit has been constructed as described above, a "Success" message will be displayed upon clicking "Submit".

4-Bit Array Multiplier

Circuit Diagram

4-Bit Array Multiplier Circuit Diagram

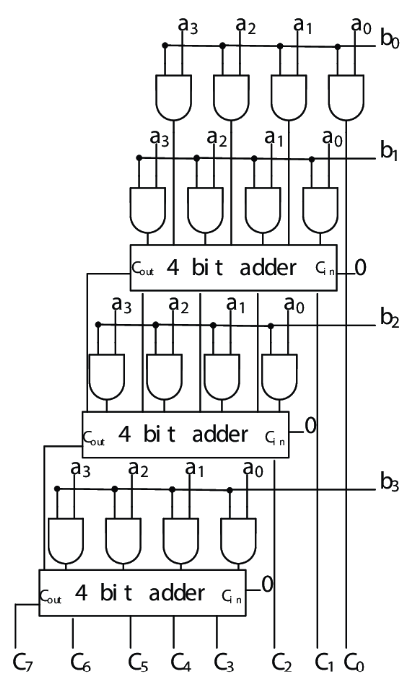
Figure 2: 4-bit array multiplier circuit diagram showing systematic partial product generation and addition stages. Reference: Theory section

Components Required

  • 16 AND gates (for 4×4 partial product matrix)
  • Multiple Half adders and Full adders for partial product summation
  • Proper carry propagation connections

Circuit Connections

  1. Create the first row of partial products by dragging 4 AND gates and connecting them as follows:
    • First AND gate: inputs A₀ and B₀ (generates P₀₀)
    • Second AND gate: inputs A₀ and B₁ (generates P₀₁)
    • Third AND gate: inputs A₀ and B₂ (generates P₀₂)
    • Fourth AND gate: inputs A₀ and B₃ (generates P₀₃)
  2. Create the second row of partial products by dragging 4 AND gates and connecting them as follows:
    • Fifth AND gate: inputs A₁ and B₀ (generates P₁₀)
    • Sixth AND gate: inputs A₁ and B₁ (generates P₁₁)
    • Seventh AND gate: inputs A₁ and B₂ (generates P₁₂)
    • Eighth AND gate: inputs A₁ and B₃ (generates P₁₃)
  3. Create the third row of partial products by dragging 4 AND gates and connecting them as follows:
    • Ninth AND gate: inputs A₂ and B₀ (generates P₂₀)
    • Tenth AND gate: inputs A₂ and B₁ (generates P₂₁)
    • Eleventh AND gate: inputs A₂ and B₂ (generates P₂₂)
    • Twelfth AND gate: inputs A₂ and B₃ (generates P₂₃)
  4. Create the fourth row of partial products by dragging 4 AND gates and connecting them as follows:
    • Thirteenth AND gate: inputs A₃ and B₀ (generates P₃₀)
    • Fourteenth AND gate: inputs A₃ and B₁ (generates P₃₁)
    • Fifteenth AND gate: inputs A₃ and B₂ (generates P₃₂)
    • Sixteenth AND gate: inputs A₃ and B₃ (generates P₃₃)
  5. Connect P₀₀ directly to output bit P₀.
  6. Use Half Adders and Full Adders to sum the partial products column-wise:
    • Column 1: Use Half Adder to add P₀₁ and P₁₀, connect Sum to P₁ and Carry to next stage
    • Column 2: Use Full Adder to add P₀₂, P₁₁, and carry from column 1, connect appropriately
    • Continue this pattern for remaining columns, ensuring proper carry propagation
  7. Connect the final outputs to P₇P₆P₅P₄P₃P₂P₁P₀.
  8. Set the input values for A₃A₂A₁A₀ and B₃B₂B₁B₀, then click "Simulate".

Observations

  • The output P₇P₆P₅P₄P₃P₂P₁P₀ represents the 8-bit product of two 4-bit numbers.
  • Maximum product: 15 × 15 = 225 = 11100001₂
  • The array multiplier provides a systematic approach to binary multiplication with predictable timing.
  • If the circuit has been constructed correctly with proper carry connections, a "Success" message will be displayed upon clicking "Submit".

4-Bit Advanced Multiplier

Circuit Diagram

4-Bit Advanced Multiplier Circuit Diagram

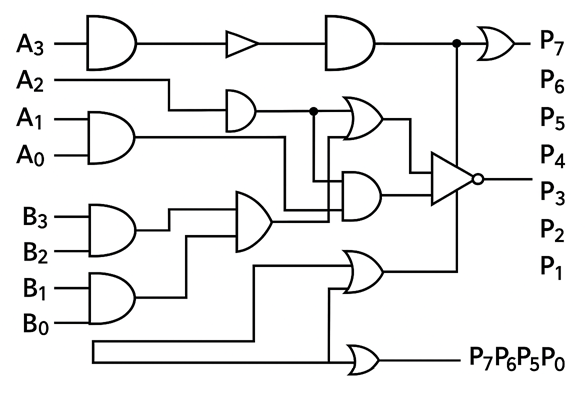
Figure 3: 4-bit advanced multiplier circuit diagram showing optimized implementation with additional logic gates. Reference: Theory section

Components Required

  • 16 AND gates (for partial product generation)
  • Multiple Half adders and Full adders
  • NOT gates for signal inversion and optimization
  • XOR and OR gates for enhanced logic operations

Circuit Connections

  1. Follow the same partial product generation steps as the 4-Bit Array Multiplier (steps 1-4 above).
  2. Implement optimized addition network using available logic gates:
    • Use NOT gates for signal inversion where beneficial
    • Employ XOR gates for sum generation in custom adder configurations
    • Utilize OR gates for optimized carry generation
  3. Connect the addition network with proper carry propagation, taking advantage of the extended gate library for optimization.
  4. Ensure all partial products are properly summed and connected to output bits P₇P₆P₅P₄P₃P₂P₁P₀.
  5. Set the input values for A₃A₂A₁A₀ and B₃B₂B₁B₀, then click "Simulate".

Observations

  • The circuit demonstrates advanced multiplier design techniques with optimized logic.
  • Output P₇P₆P₅P₄P₃P₂P₁P₀ represents the same 8-bit product but with potentially improved characteristics.
  • Students can explore different optimization strategies using the available gate library.
  • If the circuit has been constructed correctly, a "Success" message will be displayed upon clicking "Submit".

Wallace Tree Multiplier

Circuit Diagram

Wallace Tree Multiplier Circuit Diagram

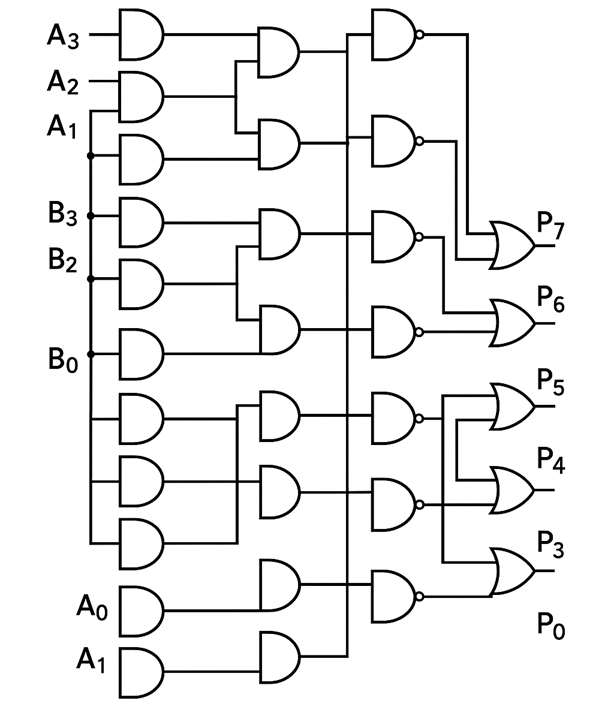
Figure 4: Wallace tree multiplier circuit diagram showing parallel reduction tree structure for high-speed multiplication. Reference: Theory section

Components Required

  • 16 AND gates (for partial product generation)
  • Multiple Half adders and Full adders arranged in tree structure
  • Complete logic gate library (AND, OR, XOR, NOT, NAND, NOR) for optimization
  • Proper tree-structured carry-save addition network

Circuit Connections

  1. Generate all 16 partial products using AND gates as in previous implementations (steps 1-4 from 4-Bit Array Multiplier).
  2. Implement Wallace tree reduction:
    • Group partial products into sets of three and use Full Adders for 3:2 compression
    • Group remaining pairs and use Half Adders for 2:2 compression
    • Continue reduction stages until only two operands remain
  3. Use the complete gate library for optimization:
    • NAND gates can replace AND-NOT combinations for area efficiency
    • NOR gates can replace OR-NOT combinations
    • Implement custom logic using universal gates where beneficial
  4. Implement final ripple carry adder or carry lookahead adder for the last two operands.
  5. Connect the final outputs to P₇P₆P₅P₄P₃P₂P₁P₀.
  6. Set the input values for A₃A₂A₁A₀ and B₃B₂B₁B₀, then click "Simulate".

Observations

  • The Wallace tree structure minimizes the critical path delay through parallel processing.
  • Output P₇P₆P₅P₄P₃P₂P₁P₀ represents the 8-bit product with optimized timing characteristics.
  • The tree structure trades area for speed, demonstrating important design trade-offs.
  • Advanced students can explore different tree configurations and optimization techniques.
  • If the circuit has been constructed correctly with proper tree structure, a "Success" message will be displayed upon clicking "Submit".