The z- transform for a discrete-time signal x[n] is given as:
X(z)=n=−∞∑∞x[n] z−n
where X(z) is a complex valued function of complex variable z.
z transform always has two parts:
(i) Mathematical expression X(z)
(ii) Region of convergence (ROC) - region in z- plane where the sum of X(z) converges.
Examples:
(i) Let x[n] be δ[n]={1 n=00otherwise
We know that z- tranform can be given as:
X(z)=∑n=−∞∞x[n] z−n
=∑n=−∞∞δ[n] z−n
=1
ROC of δ[n] : whole z-plane
(ii) x[n]=δ[n−n0], where n0>0 and an integer
We know that z- tranform can be given as:
X(z)=∑n=−∞∞x[n] z−n
=∑n=−∞∞δ[n−n0] z−n
=z−n0
=(z1)n0
ROC: whole z-plane except z=0
(iii) x[n]=δ[n+n0], where n0>0 and an integer
We know that z- tranform can be given as:
X(z)=∑n=−∞∞x[n] z−n
=∑n=−∞∞δ[n+n0] z−n
=zn0 using shifting property of impulse signals
ROC: whole z-plane except ∣z∣=∞
Poles and zeros
We are interested in z-transform in the form of ratio of polynomials in z
X(z)=D(z)N(z)
Numerator N(z)=0 provides zeros of X(z)
X(z)=0
Denominator D(z)=0 provides poles of X(z)
X(z)=∞
Note
Poles play an important role in deciding the ROC, zeros do not. The ROC can not contain any poles.
Different time domain signals can have same z-transform expression X(z)
but with different ROC.
Example:
1. x[n]=anu[n]
X[z]=∑n=−∞∞x[n] z−n
X[z]=∑n=−∞∞anu[n] z−n
X(z) = z−az ;
x[n] is a causal signal i.e. x[n]=0 for n<0
ROC: ∣z∣>∣a∣
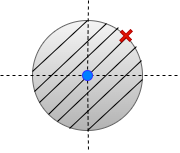
2. x[n]=−anu[−n−1]
X[z]=∑n=−∞∞x[n] z−n
X[z]=∑n=−∞∞−anu[−n−1] z−n
X(z) = z−az ;
x[n] is a anti-causal signal i.e. x[n]=0 for n>0
ROC: ∣z∣<∣a∣