Wien's bridge is an ac electrical circuit widely used for the measurement of capacitance with high accuracy and can also be used for measuring frequency. The circuit consists of four arms, two arms with a series combination of resistors and capacitors and the other two arms have resistors. The circuit diagram of Wien's bridge is shown below:

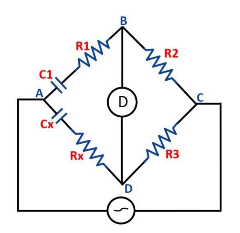
Fig.1 Wein's Bridge

A balance detector or null indicator is connected across two junctions (i.e., across BD as shown above). The indicator shows null deflection when the bridge is balanced i.e., When the junctions B and D will be at the same potential.

Let Z1, Z2, Z3, and Z4 be the impedances of the arm AB, BC, CD, and AD respectively, and given as-

$$ Z1 = R1 + \frac{1}{jωC1} $$

$$ Z2 = R2 $$

$$Z3 = R3$$

$$ Z4 =Rx + \frac{1}{jωCx} $$

When the bridge is balanced, We have,

$$ Z1Z3 = Z2Z4 $$

$$\frac{R2}{R3} = \frac{R1 + \left (\frac{1}{jωC1} \right )}{Rx + \left (\frac{1}{jωCx} \right )}$$

$$ R2Rx + \left (\frac{R2}{jωCx} \right ) = R1R3 + \left (\frac{R3}{jωC1} \right )$$

Now, Equating the Real and Imaginary terms,

$$ R2Rx = R1R3 $$

$$ Rx = \frac{R1R3}{R2}…. (1) $$

$$ \frac{R2}{jωCx} = \frac{R3}{jωC1} $$

$$ \frac{R2}{Cx} = \frac{R3}{C1} $$

$$ Cx = \frac{C1R2}{R3}.... (2) $$

The above equations are used to determine the unknown resistance and Capacitance respectively.

Applications of Wein's Bridge:

1. Wien's bridge is used for measurement of capacitance in terms of resistance and frequency.
   

2. It can also be used to measure audio frequencies.
   

3. The Wien’s bridge is suitable for the measurement of frequency of the range of 100Hz to 100kHz.