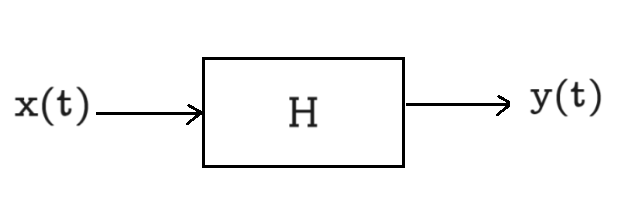
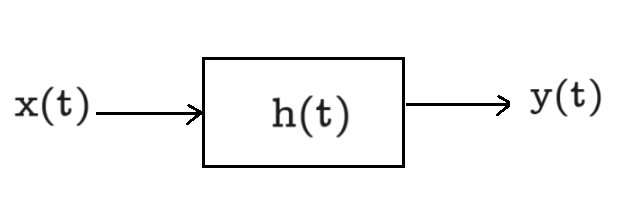System Stability
Stable Systems
There are many notions of a stable system. Here we consider stability based on boundedness of input and output signals as defined next. A system is said to be stable if for any bounded input, the output is also bounded, i.e., bounded input bounded output (BIBO) stability.
If , then for BIBO stability we must have,
Similarly, a discrete time system is said to be BIBO stable if any bounded input signal gives a bounded output signal.
If , then for BIBO stability,
Examples
Solution:
Solution:
LTI systems with BIBO Stability
It can be shown that a linear and time invariant (LTI) system is BIBO stable if and only if ,i.e., the impulse response is absolutely integrable. Similarly, for a discrete time LTI system, BIBO stability implies that the impulse response is absolutely summable, i.e., .
Example
Find values of the complex parameter for which the discrete time LTI system with impulse response is stable.
Solution:
which converges only when . Thus the system is stable when the complex parameter is inside the unit circle in the complex plane.
LTI system transfer function
Let an LTI system have rational transfer function given by,
For a causal system, the stability of the above system depends completely on the location of its poles. Specifically, for the system to be stable, all the poles should lie on the left half plane.
PID Controller
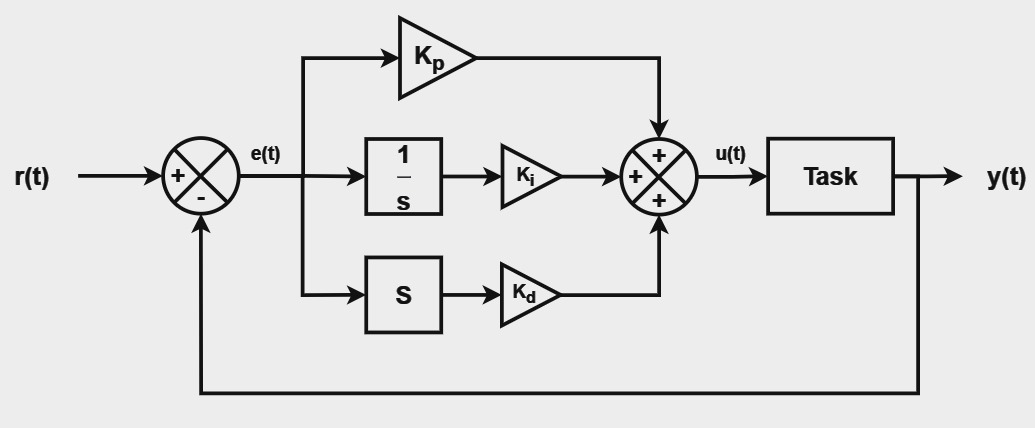
A commonly used second order system is the Proportional–integral–derivative (PID) controller. A PID system block diagram is shown above. It is a feedback system with system function governed by the constants and . The system function and the corresponding poles and zeros are given by,
The stability of the system depends on the parameters and .