Theory: The time response has utmost importance for the design and analysis of control systems because these are inherently time domain systems where time is independent variable. During the analysis of response, the variation of output with respect to time can be studied and it is known as time response. To obtain satisfactory performance of the system with respect to time must be within the specified limits. From time response analysis and corresponding results, the stability of the system, accuracy of the system, and complete evaluation can be studied easily. Due to the application of an excitation to a system, the response of the system is known as time response and it is a transient response; steady-state response.

Transient Response: The part of the time response which goes to zero after large interval of time is known as transient response.
Steady State Response: The part of response that means even after the transients have died out is said to be steady state response.

The total response of a system is sum of transient response and steady state response.
C(t)=C_tr(t) + C_ss(t)

Time Response Specification Parameters: The transfer function of 2_nd order system is generally represented by the following transfer funnction:

The dynamic behavior of the second order system can then be described in terms of two parameters: the dumping ratio and the natural frequency.
If the dumping ratio is between 0 and 1, the system poles are complex conjugates and lie in the left half s plane. The system is then called underdamped, and the transient response is oscillatory . If the damping ratio is equal to 1 the system is called critically damped , and when the damping ratio is larger than 1 we have overdamoed system. The transient response of critically damped and overdamped systems do not oscillate. If the damping ratio is 0, the transient response does not die out.

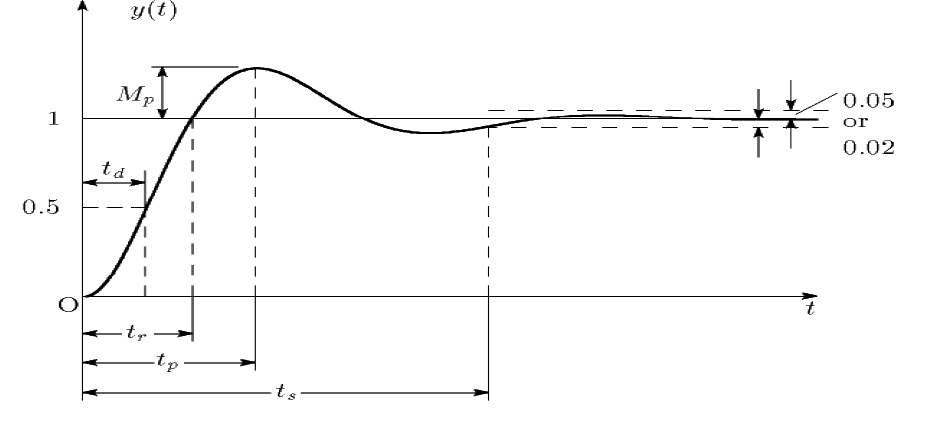Delay time (t_d): Yhe delay time is the time required for the reponse to reach half the final value the very first time.
Rise Time (t_r): The rise time required for the response to rise from 10% to 90%, 5% to 95%, or 0% to 100% of its final value. For the underdamped second order systems, the 0% to 100% rise time is normally used. For overdamped systems, the 10% to 90% rise time is commonly used.
Peak time (t_p): The peak time is time required for the response to reach the first peak of overshoot. Maximum (percent) overshoot (M_p): The maximum overshoot is the maximum peak value of the response curve measured from unity. If the final steady-state value of the response differs from unity, then it is common to use the maximum percent overshoot. It is defined by:

Settling time: The settling time is the time required for the response curve to reach and stay within a range about the final value of size specified by absolute percentage of the final value (usually 2% or 5%). The sttling time is related to the largest constant of the control system.