To Study the Wien Robinson's frequency Bridge 
Theory
#1 To calibrate the dial makring of signal generator by employing the Wien Robinson's bridge.
#2 To determine the response of the bridge with frequency varitation, when the bridge is set for 1000 Hz.
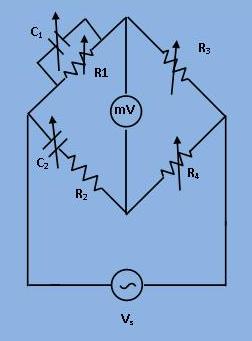
Circuit Diagram
It is ratio real type bridge, for balance we have
$$\frac{R_1}{1 + j\omega C_1 R_1} * R_4 = (R_2 - \frac{j}{\omega C_2}) * R_3$$
$$\frac{R_4}{R_3} = \frac{R_2}{R_1} + \frac{C_1}{C_2} + j (\omega C_1 R_2 - \frac{1}{C_2 R_2})-----(1)$$
Equating real and imaginary parts of eq.(1), we have
$$\frac{R_4}{R_3} = \frac{R_2}{R_1} + \frac{C_1}{C_2}-----(2)$$
and
$$\omega C_1R_2 - \frac{1}{\omega C_2R_1} = 0------(3)$$
from eq.(3) we get omega (w) as
$$\omega = \frac{1}{\sqrt{R_1R_2C_1C_2}}$$
if in eq. (2) we consider
$$R_1 = R_2 and\ $$
$$C_1 = C_2$$
then we get the frequency (f) and another useful resistance ratio as
$$f = \frac{1}{2 \pi \sqrt{R_1R_2C_1C_2}} and$$
$$\frac{R_4}{R_3} = 2$$
