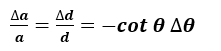Errors in measurement of interplanar spacing d and lattice parameter(s) a using modern diffractometers can occur due to :

• Misalignment of the instrument
  
• Absorption of X-Rays by the specimen
  
• Displacement of the specimen from the diffractometer axis must be minimized (observational error)
  
• Vertical divergence of the incident beam
  
• Use of a flat specimen instead of a curved one to correspond to the diffractometer circle
  
  

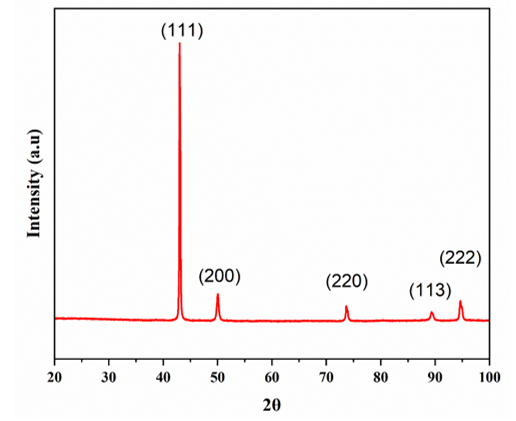
Figure 1: X-Ray Diffractogram for an FCC material

Observational error :

• For a cubic material :
  
  

Where the d-spacing is measured from Bragg’s law :

Here, n = 1 which is the first order of diffraction and λ = 1.5406 Å for Cu-K_α radiation.

• Precision in measurement of a or d depends on precision in derivation of sinθ.
  
  

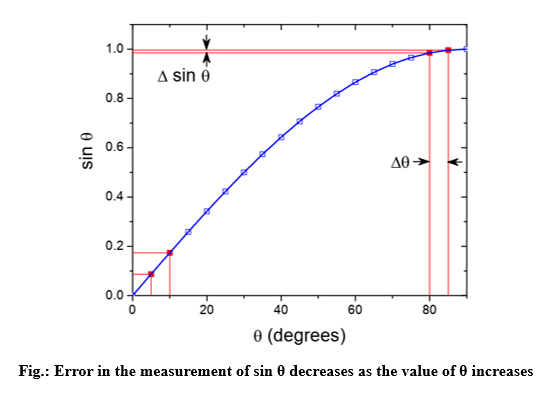
Figure 2: Error in the measurement of sin θ decreases as the value of θ increases

• Take partial derivative of the Bragg equation :
  
  
  
  

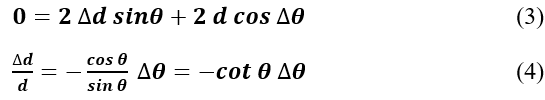
• For a cubic system :
  
  
  
  

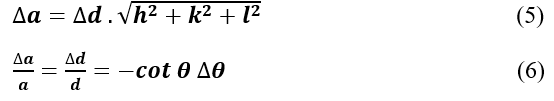
• The term ∆a⁄a (or ∆d⁄d) is the fractional error in a (or d) caused by a given error in θ. The fractional error approaches zero as θ approaches 90°.
  
  

• Values of a will approach the true value as we approach 2θ = 180° (i.e., θ = 90°). We can’t measure a value at 2θ = 180°. We must plot measured values and extrapolate to 2θ = 180° versus some function of θ.
  
  

Absorption Error :

• For a cubic crystal with a lattice parameter a, a Nelson-Riley extrapolation function is used :