Theory

Norton's Theorem:

Norton's theorem states that a network consisting of several voltage sources, current sources, and resistors with two terminals is electrically equivalent to an ideal current source I_NO and a single parallel resistor R_NO. The theorem can be applied to both A.C. and D.C. cases.

The Norton equivalent of a circuit consists of an ideal current source in parallel with an ideal impedance (or resistor for non-reactive circuits).

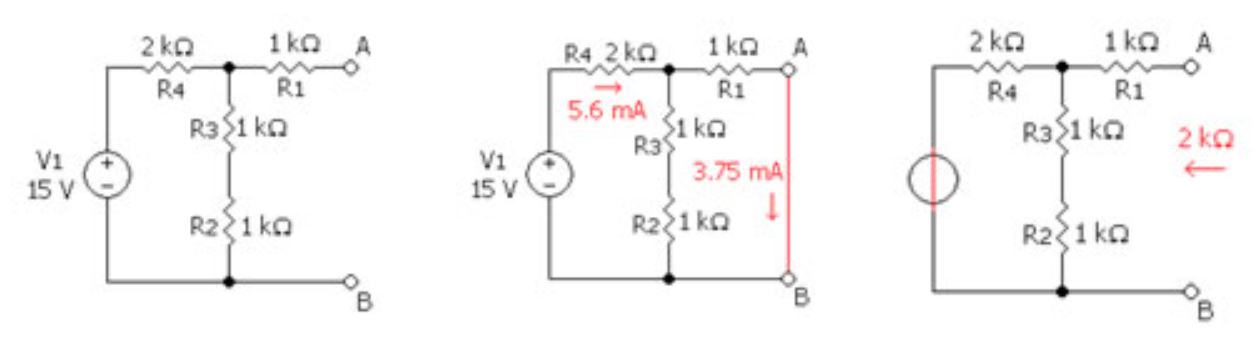
Norton Equivalent Circuit:

The Norton equivalent circuit is a current source with current I_NO in parallel with a resistance R_NO. To find its Norton equivalent circuit:

1. Find the Norton current (I_NO):
   Calculate the output current, I_AB, when a short circuit is the load (i.e., 0 resistance between A and B). This current is I_NO.
2. Find the Norton resistance (R_NO):
   If there are no dependent sources, you can use one of the following methods:
   • Calculate the output voltage, V_AB, under open circuit condition (no load connected). Then, R_NO = V_AB / I_NO.
   • Replace independent voltage sources with short circuits and independent current sources with open circuits. Then calculate the resistance seen at the output terminals; this is R_NO.
3. When dependent sources are present:
   Use the general method:
   • Connect a 1 Ampere constant current source across the output terminals.
   • Calculate the resulting voltage across this source.
   • The Norton resistance is R_NO = V / 1 A.
   • This method is valid for all circuits and is required when dependent sources exist.

Example 1:

Consider this circuit –

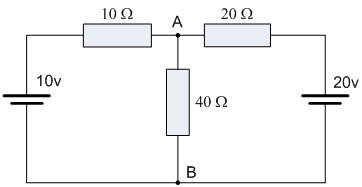
To find the Norton’s equivalent of the above circuit, we first remove the center 40Ω load resistor and short the terminals A and B. This gives us the following circuit:

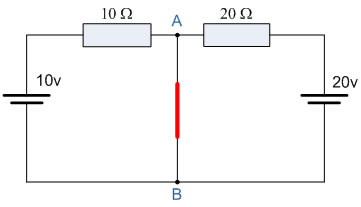
When the terminals A and B are shorted together, the two resistors are connected in parallel across their respective voltage sources. The currents flowing through each resistor, as well as the total short-circuit current, can now be calculated as:

$$I_1 = \frac{10\,\mathrm{V}}{100\,\Omega} = 1\mathrm{A}, \quad I_2 = \frac{20\,\mathrm{V}}{200\,\Omega} = 1\mathrm{A}$$

therefore,

$$I_{\text{short-circuit}} = I_1 + I_2 = 2\mathrm{A}$$

If we short out the two voltage sources and open circuit terminals A and B, the two resistors are now effectively connected together in parallel. The value of the internal resistor R_S is found by calculating the total resistance at the terminals A and B, giving us the following circuit:

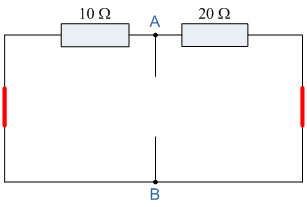
Find the Equivalent Resistance (R_S):

10Ω resistor in parallel with the 20Ω resistor.

$$R_T = \frac{R_1 \times R_2}{R_1 + R_2} = \frac{20 \times 10}{20 + 10} = 6.67\,\Omega$$

Having found both the short-circuit current, I_S, and the equivalent internal resistance, R_S, this gives us the following Norton's equivalent circuit:

Nortons equivalent circuit.

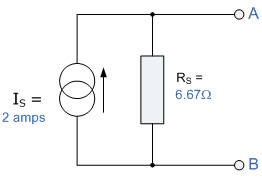
Ok, so far so good, but we now have to solve with the original 40Ω load resistor connected across terminals A and B, as shown below.

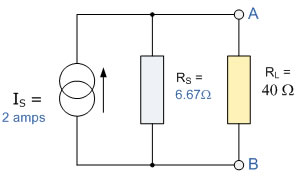
Again, the two resistors are connected in parallel across the terminals A and B, which gives us a total resistance of:

$$R_T = \frac{R_1 \times R_2}{R_1 + R_2} = \frac{6.67 \times 40}{6.67 + 40} = 5.72\Omega$$

The voltage across the terminals A and B with the load resistor connected is given as:

$$V_{y\text{-}g} = 1 \times R = 2 \times 5.72 = 11.44\mathrm{V}$$

Then the current flowing in the 40Ω load resistor can be found as:

$$I = \frac{V}{R} = \frac{11.44\,\mathrm{V}}{40\,\Omega} = 0.29\,\mathrm{A}$$

Verification of Norton’s Theorem using the simulator:

Step 1: Create the actual circuit and measure the current across the load points.

Step 2: Create the Norton’s equivalent circuit by first creating a current source of the required equivalent current in amperes (2 A in this case), and then measure the current across the load using an ammeter.

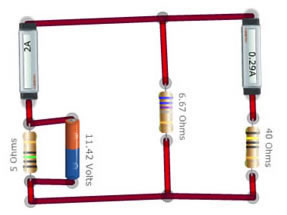
In both cases, the current measured across the resistance should be the same.

More about Norton’s Theorem:

1. Norton’s theorem and Thevenin’s theorem are equivalent, and this equivalence leads to source transformation in electrical circuits.
2. For an electric circuit, the equivalence is given by:
   
   VTh = INo × RTh
   
   i.e., Thevenin’s voltage = Norton’s current × Thevenin’s resistance
3. The applications of Norton’s theorem are similar to those of Thevenin’s theorem. The main application is the simplification of electrical circuits using source transformation.