Given an input image f(x,y) an output image g(x,y) is computed by applying some operation on a local neighbourhood N of each pixel in the image f. This can be visualized as follows: a window or mask is placed at every pixel location in f(x,y) and some operation is performed on the pixels within the window. The window is moved to the next pixel location nd the process is repeated. Thus,

Where HN is the neighborhood operator of size N and g is the output image.

Linear operations :

Linear operations can be represented as a convolution operation between f(x,y) and a window function w(x,y) as follows.

w is a window function which in practice is in the form of a matrix of size s x t; a=(s-1)/2 and b=(t-1)/2 .

An example of 3x3 w(x,y) is shown below.

An example of convolution operation is shown below:

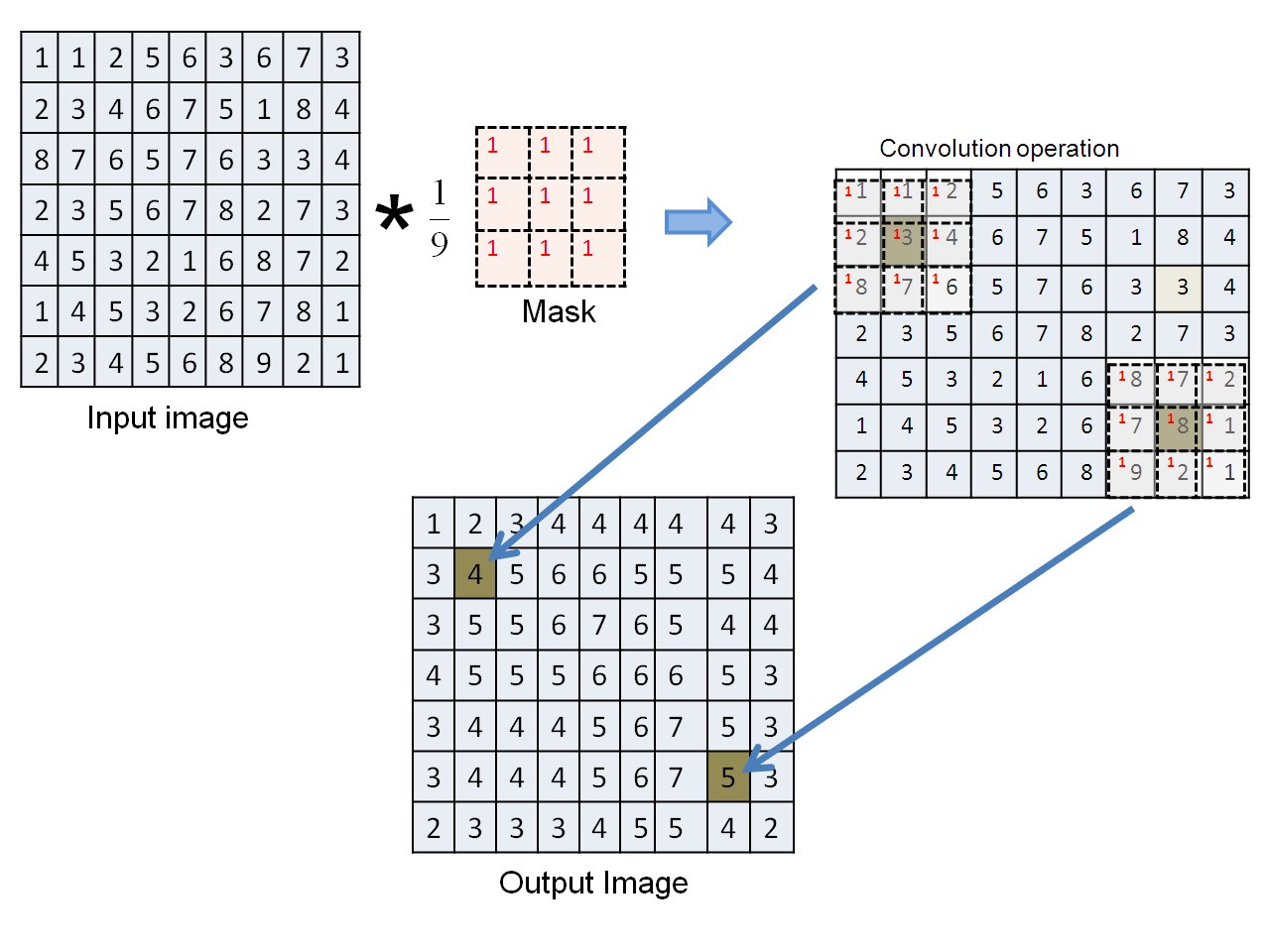
Note that w(0,0) is the coefficient or weight of the window function at the centre which is the position of the current pixel in f(x,y). Varying the weights w(i,j), results in different type of linear neighborhood operations. The above operations are generally termed as filtering operations and w is referred to as a filter. A popular filter is one which performs local averaging or smoothing of the image. This is a low pass filter. The key characteristic of this filter is that w(i,j) > 0 for every (i,j). An additional constraint is generally imposed on the weights to sum to 1. Below are some examples.

1. Straight averaging filter: All the filter coefficients are equal.

2. Triangular filter:All the coefficients are arranged to form a pyramid (with triangular faces) as shown below

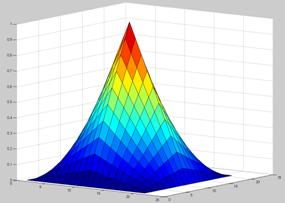
3. Gaussian filter: The filter coefficients form a bell shaped surface as shown below.

Nonlinear Operations:

Nonlinear Operations:

H_N can also be a nonlinear operator. An example is one which performs a ranking operation. Such operations cannot be represented as a convolution between f(x,y) and a window function as in the case of linear operations.

1. Median filter: The operator HN computes the median of the set of grey values in the neighborhood of the current pixel in f(x,y). This is found by performing a sorting operation at every location (x,y) in f(x,y).
2. Unsharp Masking filter: This is another example of nonlinear filtering. Here, the aim is to highlight the details. This operation is given by

Where is the result of applying an averaging filter (ex. Gaussian) to the input f(x,y) and a < 1 is a constant. Note that if a =1 then we have an operation that will retain only the details in the image.

Implementation Issues

When a pixel lies in the border of the input image, some elements of its neighbourhood is not defined. Hence the mask cannot be applied. To circumvent this issue, one of the following two approaches can be used :

Zero Padding : The undefined pixels are assumed to be zero and the mask can be applied. For example: An input image of size MXN and filter size mXn, the output image size will be (M+(m-1)/2) X (N+(n-1)/2)

Repetition : The border pixels in input image are repeated, so that the neighbourhood is always defined and mask can be applied.

An example demonstrating Zero-Padding and repitition of border pixels is shown below: