Minimum Spanning Trees

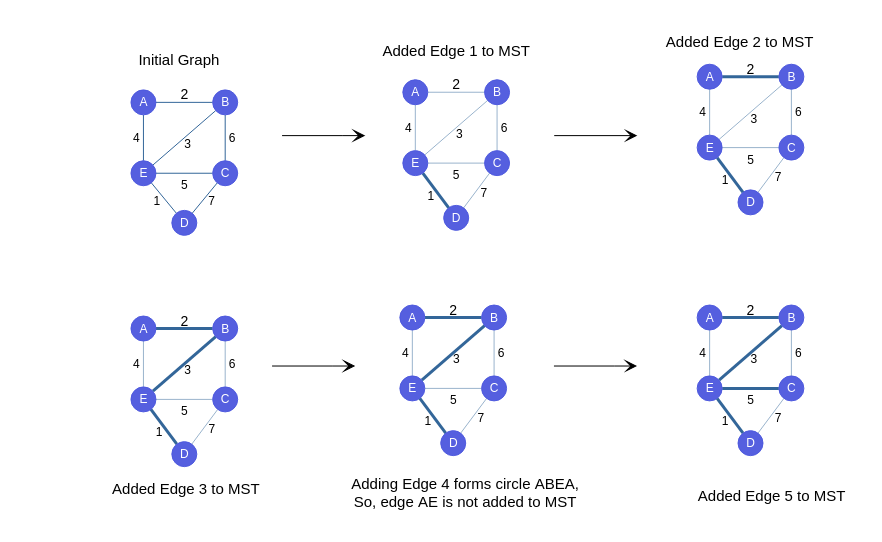
Let's have a final look at the consolidated algorithm to find MST of given graph:

STEP 1 : Sort the given edges
STEP 2 : Check each edge in sorted order if it forms a cycle with already selected edges. If not Add it to list of MST . If it does move to next edge.
STEP 3 : Run steps 1 and 2 till v-1 edges are selected (v=no.of.vertices).

From the mentioned Algo, we can conclude that after the T^th iteration, we will have the edges which should be in MST among T smallest places included in MST.
So, After N iterations we will have all edges which are to be in MST included in it.
Notice that after including N-1 edges in MST , MST will be finished.
Look at the picture below and work out the result of each iteration. See if it matches the picture, and notice which elements keep getting placed correctly after each iteration!