Minimum Spanning Trees

How can we find MST using Kruskal's?

Kruskal's Algorithm is a classic method for finding the Minimum Spanning Tree (MST) of a graph.

• First, sort all edges of the graph in increasing order of their weights.
• Check each edge in sorted order to see if it should be included in the MST.
• If adding an edge would create a cycle (detected using Union-Find), skip it; otherwise, add it to the MST.
• Repeat until the MST contains exactly N-1 edges (where N is the number of vertices).

Note: Each edge is considered only once, and the MST is built by always choosing the smallest available edge that does not form a cycle.

When should we add an edge to the MST?

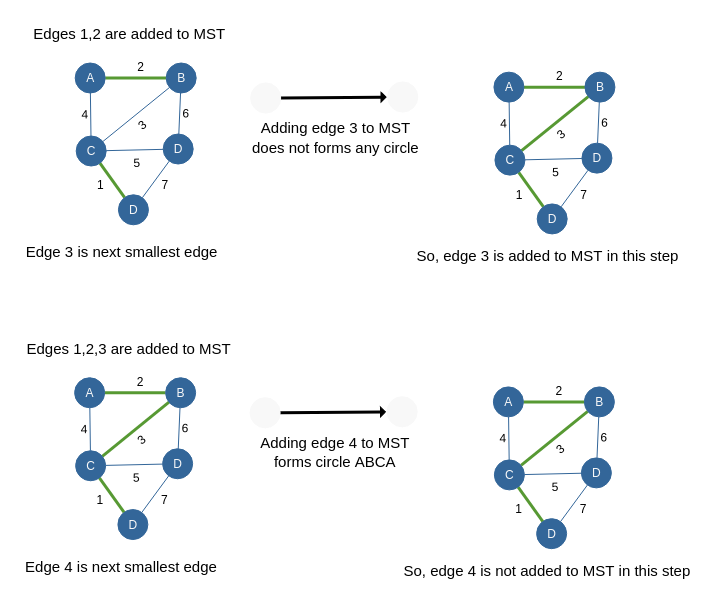
Important Observations

• After each iteration, the smallest available edge that does not form a cycle is added to the MST.
• After N-1 edges are included, the MST is complete.
• Work through each step and see which edges are included.

Step by Step Process for Kruskal's

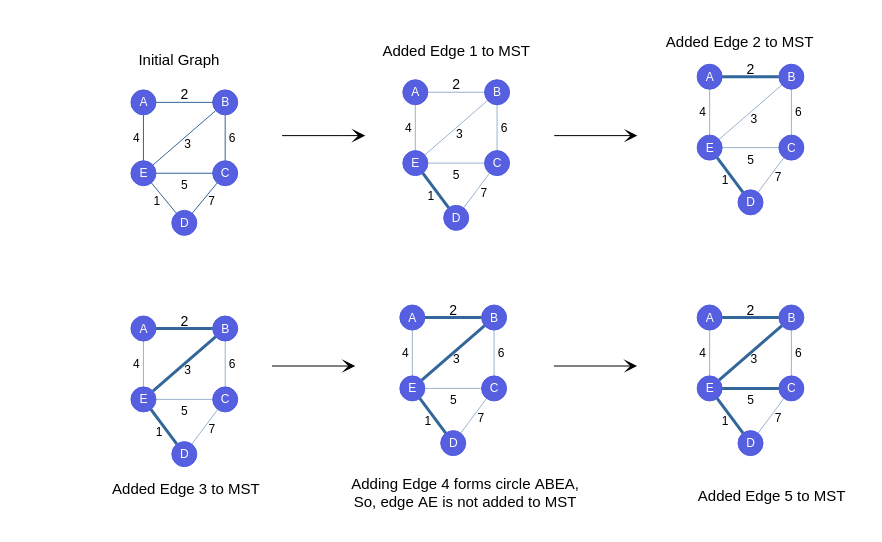
Tip: Make sure all vertex names in your diagrams are unique to avoid confusion.