Reaction kinetic studies in a mixed flow reactor
Background and Theory
Flow Reactors :
There are two types of flow reactors in common use in the chemical industry. They are the continuous stirred tank reactor (CSTR) and the tubular reactors. CSTR or Mixed flow reactor(MFR) is configured much like a batch reactor except reactants and products continuously flow in and out of the reactor. Steady state flow reactors are ideal for industrial purposes when large quantities of material are to be processed and when the rate of reaction is fairly high to extremely high. Flow reactors need more supporting equipment like pumps. But good product quality can be obtained.
Theory :
The continuous stirred-tank reactor (CSTR), also known as back mix reactor, is a common ideal reactor type in chemical engineering. Perfect mixing is assumed in case of Ideal CSTR .
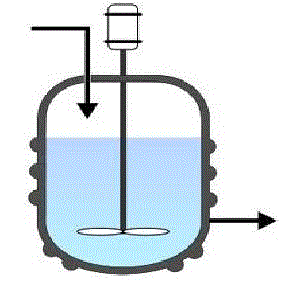
In a perfectly mixed reactor, the output composition is identical to the
composition of the material inside the reactor, which is a function of
residence time and rate of reaction. The ideal CSTR model is often used to
simplify engineering calculations and can be used to describe research
reactors. In practice it can only be approached, in particular in industrial
size reactors.
Space time (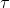 ) is the time required to process one reactor volume of feed at
specified condition.
) is the time required to process one reactor volume of feed at
specified condition.
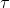 =V/volumetric flow rate of feed
=V/volumetric flow rate of feed
Mass Balance Equation :
rate of input - rate of output- rate of disappearance = rate of accumulation
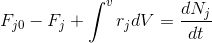
There are some basic assumptions made in analysing CSTR reactors. These are
- The reactor runs at steady state i.e. all of the time derivatives go to zero.
- None of the variables (temperature, concentration, reaction rate, etc) are functions of position, i.e. all of the spatial derivatives go to zero.
- The conditions that exist at the exit are the same as those everywhere in the reactor.
Since steady state is assumed, the dNj/dt term is equal to zero. Setting the rate term equal to a -rj, the equation can now be solved for the volume to yield
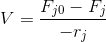
Fj0 = molar flowrate of reactant j
Fj = output molar flowrate of reactant j
rj = rate of reaction of reactant molecule j
V = volume of the reactor
Nj = number
Fi0
of moles of component j = the molar flow rate can be expressed as the product of the
concentration of the species and the volumetric flow rate (V0).
Fj0 = Cj0*v0
The design equation for CSTR is given by
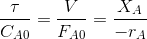 ------(A)
------(A)
Volume of a CSTR with given influent flow rate and feed composition
to achieve a required conversion may be obtained from the above
equation, if the rate equation is known. -rA in the above equation
correspond to the exit conversion or concentration.
Rate equation for a given reaction can be obtained using a CSTR.
For a single reaction say, A+B-->C+D
Assume the rate equation to be 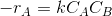 and a constant density system
Experiments to be performed with different space times in the reactor with
the known ratio of reactant B to A(M) in the inlet. Steady state
concentration of A may be analysed for each run.
and a constant density system
Experiments to be performed with different space times in the reactor with
the known ratio of reactant B to A(M) in the inlet. Steady state
concentration of A may be analysed for each run.
Now equation A can be written as
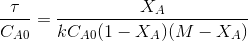 ------(B)
------(B)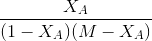 Plotting
vs
Plotting
vs 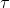 yields a straight line passing through origin if
the assumed equation is correct. The slope=k. The equation holds good for
M=1 or greater than 1.
yields a straight line passing through origin if
the assumed equation is correct. The slope=k. The equation holds good for
M=1 or greater than 1.If the data do not fit by a straight line assume different equation and proceed as above.
