Given samples of a class, x₁, x₂, ... x_n, each being an d-dimensional vector, we define the mean, μ, and the covariance matrix, Σ are defined as:

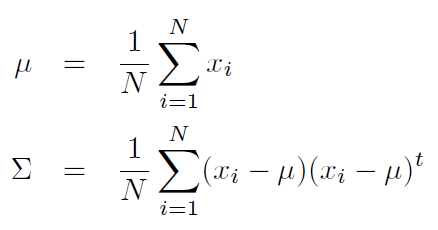
Properties of μ and Σ

1. Note that xis are d-dimensional column vectors, and hence the mean, μ, is also a d-dimensional column vector. The covariance matrix, Σ, is a dxd symmetric square matrix.
2. The mean, μ is the centroid of the samples in the feature space.
3. The covariance matrix, Σ is a positive semi-definite matrix.