Theory:

A Boolean expression is an expression consists of binary variables and logical operators that evaluates to either true or false. A Boolean expression could be implemented with logic gates. To use the minimum number of logic gates, Boolean expressions could be simplified using different techniques. This refers to the process of reducing Boolean expressions to their simplest form using identities, laws, and postulates. Following five key postulates by Edward V. Huntington form the basis for all simplifications and logic circuit design using Boolean algebra.

1. Closure:
   For any two elements in the set (usually {0, 1}), the results of AND (.), OR (+), and NOT ( ' ) operations are also within the set.
2. Identity Elements:
   There exist unique elements 0 and 1 such that for any element x: x + 0 = x and x . 1 = x.
3. Commutativity:
   The order of operands does not affect the result of AND and OR operations: x + y = y + x and x . y = y . x.
4. Distributivity:
   The OR operation distributes over the AND operation, and vice-versa: x + (y . z) = (x + y) . (x + z) and x . (y + z) = (x . y) + (x . z).
5. Complementation:
   For every element x, there exists a complement x' such that x + x' = 1 and x . x' = 0.

A simplified Boolean expression uses the fewest gates possible to implement a given expression.

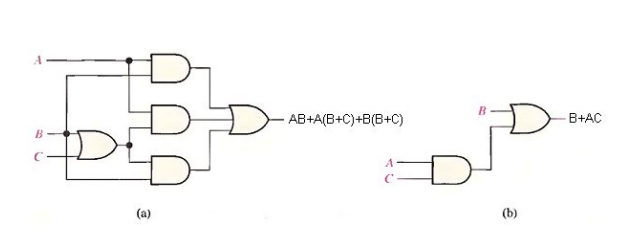
Example Using Boolean algebra techniques, simplify this expression:

$$AB + A(B + C) + B(B + C)$$

Solution:

1. Step 1: Apply the distributive law to the second and third terms in the expression, as follows:

$$A B + A B + A C + B B + B C$$

2. Step 2: Apply rule 7 (BB = B) to the fourth term.

$$AB + AB + AC + B + BC$$

3. Step 3: Apply rule 5 (AB + AB = AB) to the first two terms.

$$AB + AC + B + BC$$

4. Step 4: Apply rule 10 (B + BC = B) to the last two terms.

$$AB + AC + B$$

5. Step 5: Apply rule 10 (AB + B = B) to the first and third terms.

$$B+AC$$

At this point the expression is simplified as much as possible.