KMP Algorithm
Why we need String Searching?
- Surprisingly, strings are more often used in computer science than numbers. May it be editing text documents in word processors, reading our favourite blogs or even a basic search on google.
- Strings are everywhere. Hence it is important to study and understand the methods to manipulate, traverse and search among them.
Real Life Applications
Efficient string searching is crucial to the way the internet functions today. They have a plethora of uses and applications:
- Spell Checkers
- Intrusion Detection systems
- Predictive Seach Engines
- Plagiarism detection
- Information Retrieval System etc.
Basic Approach
If we were to approach this problem of searching for a pattern inside a string, the first trivial solution would be a brute-force method. We will be examining this method in the next task of this learning unit.
Explanation
The brute-force method to find a pattern in a given string text is:
- Have two pointers strInd and patInd pointing at string beginning and pattern beginning.
- Compare the characters present at the pointer.
- If they match, increase both the pointers by one.
- Repeat unless all the characters of pattern match or there is a mismatch
- If all the letters of the pattern have been matched then we have found the pattern in the string.
- If there is a mismatch:
- Bring the patInd pointer back to the beginning of the pattern
- Bring the strInd pointer to the second position of the string now and Repeat the process.
- If another mismatch is encountered , bring the strInd to the 3rd position of the string and so on.
- If strInd ever increases beyond the length of the string then return 0 since it means that the pattern doesn't exist in the string.
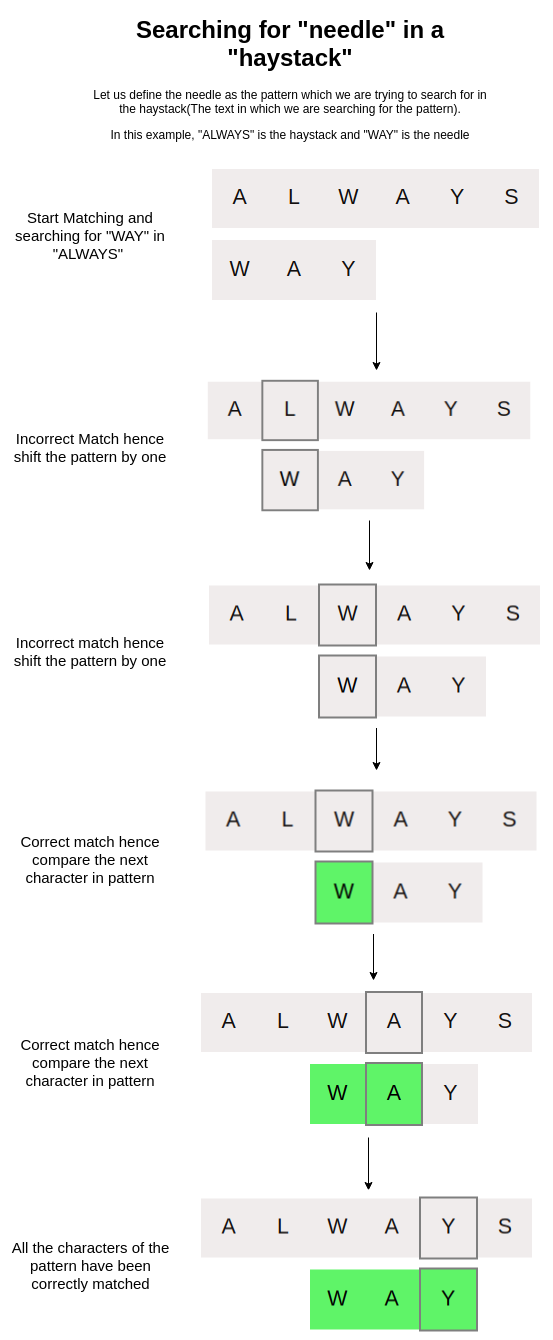
Iteration by Iteration Visualization of Naive String Searching Algorithm
Time Complexity
Note: It is recommended to see the interactive demo task before reading this.
Deciding the big O notation for any algorithm is a function of the worst-case scenario of the algorithm. Let us consider a case - the pattern of length M to be searched in a string of length N always fails on the pattern's last character and succeeds only at the end of the string.
Example :
String : AAAAAAAAAAAAAAAAAAAAAAX
Pattern : AAAAAX
Assuming that the time required to compare two characters is O(1) then the above case will take Time = O(M \times N)
Hence the naive string searching algorithm is of the complexity O(M×N)
