Electron Probe Microanalyzer (EPMA) and the Need for ZAF Correction :

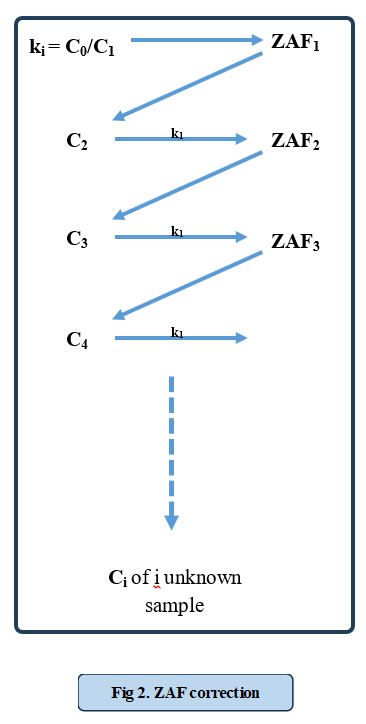
Electron Probe Microanalyzer (EPMA) is a characterization technique used to determine the precise composition of samples using Wavelength Dispersive X-ray Spectroscopy (WDS). In this technique, a focused electron beam bombards the sample, generating characteristic X-rays. These X-rays are then collimated and diffracted by analysing crystals with known lattice spacings before being collected by a detector. The entire setup is mounted on a goniometer, ensuring that the distances between the sample, diffracting crystal, and detector remain constant, as shown in figure 1

To acquire X-ray spectra over a wide wavelength range, the spectrometer contains multiple analysing crystals with different lattice spacings. Each crystal is selected based on the wavelength of the characteristic X-rays to satisfy Bragg’s law of diffraction. The commonly used analysing crystals include :

• Lithium fluoride (LiF (200)) – Small lattice spacing (0.4 nm), used for elements from Ca to Ge
• Pentaerythritol (PET (002)) – Medium lattice spacing (0.87 nm), used for elements from Si to Ti
• Thallium acid phthalate (TAP (100)) – Large lattice spacing (2.6 nm), used for elements from O to Al
• LSM80E – Very large spacing (7.8 nm), used for elements from B to O

Once the characteristic X-rays are diffracted, they are detected and converted into an intensity spectrum, representing the chemical composition of the sample. However, to ensure accurate quantification, raw data must be corrected for matrix effects using the ZAF correction model.

Need for ZAF Correction :

The measured X-ray intensities do not directly correspond to element concentrations due to interactions within the sample matrix. The three main correction factors in the ZAF model are :

• Atomic Number Effect (Z) : The atomic number effect in quantitative X-ray analysis is influenced by two key factors: backscattering (R) and stopping power (S), both of which determine the amount of X-ray intensity generated in a sample. The backscattering coefficient, which varies significantly with atomic number, leads to a loss of beam electrons, affecting X-ray production. For instance, in an aluminum-in-gold system, gold's higher backscattering coefficient results in underrepresentation of aluminum X-rays compared to a pure aluminum standard. Additionally, energy loss due to inelastic scattering is influenced by atomic number, with low-Z elements removing energy more efficiently than high-Z elements.

The depth-dependent X-ray generation function, φ(ρz), normalizes X-ray production by mass depth and is essential for understanding intensity distributions in different materials. The atomic number correction, Zi, is derived from the ratio of generated X-ray intensities in the specimen to those in a standard, inherently incorporating R and S effects. This correction is particularly crucial for multi-element samples, ensuring accurate compositional analysis.

• Absorption Effect (A) : Since X-rays must pass through a certain depth before reaching the detector, absorption follows an exponential decay law, where deeper-generated X-rays are more likely to be absorbed. The absorption path length (PL) depends on the take-off angle (ψ) and depth (z), following PL = z csc ψ, meaning higher ψ reduces absorption. The absorption correction factor (A) is applied using I/I₀ = exp[-(μ/ρ)(ρt)], where I/I₀ represents emitted vs. generated X-rays, and μ/ρ is the mass absorption coefficient, which varies significantly by element. Light elements like C, N, and O experience severe absorption, requiring a lower E₀ (below 10 keV) to ensure measurable emissions.

• Fluorescence Effect (F) : Photoelectric absorption ionizes inner atomic shells, leading to the emission of characteristic X-rays, which can induce secondary fluorescence if another element in the sample has a lower critical excitation energy. This effect is observed in the Fe-Ni system, where Ni Kα radiation (7.478 keV) excites Fe K radiation (7.11 keV), causing additional Fe fluorescence, contributing about 25% to Fe Kα intensity in a 10 wt% Fe – 90 wt% Ni alloy. The fluorescence correction factor Fi is generally minor in quantitative X-ray analysis but is considered in ZAF corrections alongside atomic number (Z) and absorption (A) effects.

Without these corrections, raw intensity measurements would be misleading, particularly for multi-element samples. A schematic diagram illustrating the effect of ZAF correction—showing intensity values before and after correction—would provide a clearer understanding of its impact.

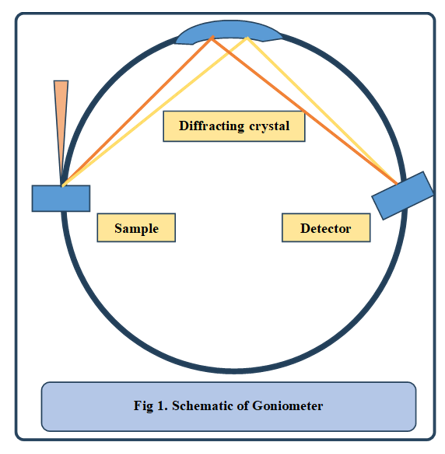
Procedure for ZAF Correction :

1. Calibration: X-ray spectra are first collected from standard samples with known compositions. These provide reference intensities and ZAF values.
   

2. K-Ratio Calculation: The ratio of X-ray intensity between the unknown sample and a standard is calculated :
   
   

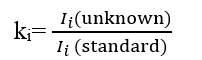
3. First Iteration: The concentration Ci is initially assumed to be linearly proportional to intensity. If deviations occur, ZAF corrections are applied iteratively.
   

4. Iterative Correction :
   • Using initial C_i, a new set of ZAF values is computed.
   • The updated ZAF values are applied to refine the concentration estimate.
   • This process repeats until C_i stabilizes, meaning further iterations produce negligible changes, as shown in figure 2.
   

5. Final Composition Mapping : Once convergence is achieved, the corrected element concentrations are reported. This process is repeated for each sample.