Virtual Labs

1. Choose the correct option for a cyclic code of length

n

, dimension

k

, and generator polynomial

\mathbf{g}(X)

a: The generator polynomial of the cyclic code need not be unique. Explanation

Explanation

b: The degree of the generator polynomial is equal to

k+1

. Explanation

Explanation

c: The generator polynomial needs to be a factor of the polynomial

X^n+1

. Explanation

Explanation

d: A linear block code

C(n,k)

is said to be a cyclic code if every vector obtained by one cyclic shift of a codeword is also a codeword in the given code

C(n,k)

. Explanation

Explanation

2. Consider two polynomial

\mathbf{f}(X) = 1+X+X^7

and

\mathbf{g}(X) = X^2+X^3+X^5

\mathbb{F}_2[X]

. What will be

\mathbf{f}(X)\mathbf{g}(X)

X^2+2X^3+X^4+X^5+X^6+X^9+X^{10}+X^{12}

Explanation

X^2+X^4+X^5+X^6+X^9+X^{12}

Explanation

1+X+X^2+X^4+X^5+X^6+X^9+X^{10}+X^{12}

Explanation

X^2+X^4+X^5+X^6+X^9+X^{10}+X^{12}

Explanation

3. Consider two polynomial

\mathbf{f}(X) = 1+X^2+X^5

and

\mathbf{g}(X) = X^3+X+1

\mathbb{F}_2[X]

. What will be the quotient (

\mathbf{q}(X)

) and remainder (

\mathbf{r}(X)

) when

\mathbf{f}(X)

divided by

\mathbf{g}(X)

\mathbf{q}(X) = X^2+X

and

\mathbf{r}(X) = X+1

Explanation

\mathbf{q}(X) = X^2+1

and

\mathbf{r}(X) = X

Explanation

\mathbf{q}(X) = X^2+X+1

and

\mathbf{r}(X) = 1

Explanation

\mathbf{q}(X) = X^3+1

and

\mathbf{r}(X) = X^2

Explanation

4. Consider the shift register based encoder for a cyclic code given in Figure 7. What will be the contents of the shift registers at the next time instant?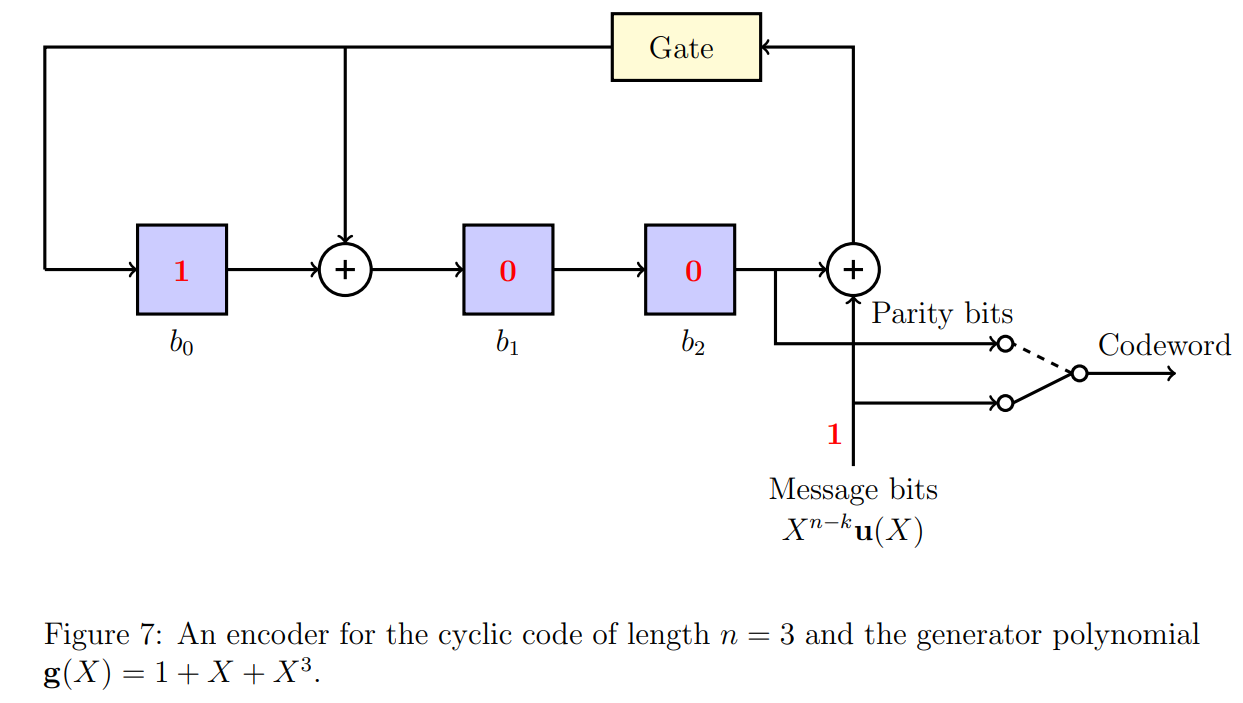

\begin{bmatrix} b_0 & b_1 & b_2 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}

Explanation

\begin{bmatrix} b_0 & b_1 & b_2 \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \end{bmatrix}

Explanation

\begin{bmatrix} b_0 & b_1 & b_2 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 \end{bmatrix}

Explanation

\begin{bmatrix} b_0 & b_1 & b_2 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0 \end{bmatrix}

Explanation

5. Consider

(7,4)

cyclic code generated by

\mathbf{g}(X) = 1 +X +X^3

. Suppose the syndrome

\mathbf{s} = \begin{bmatrix} 1 & 1 & 0 \end{bmatrix}

of a received vector

\mathbf{r} = \begin{bmatrix} r_{0} & r_{1} & r_{2} & r_{3} & r_{4} & r_{5} & r_{6} \end{bmatrix}

. Then, the syndrome of the vector

\mathbf{r}_{1}^{(1)} = \begin{bmatrix} r_{6} \oplus 1 & r_{0} & r_{1} & r_{2} & r_{3} & r_{4} & r_{5} \end{bmatrix}

\mathbf{s} = \begin{bmatrix} 0 & 0 & 0 \end{bmatrix}

Explanation

\mathbf{s} = \begin{bmatrix} 0 & 1 & 1 \end{bmatrix}

Explanation

\mathbf{s} = \begin{bmatrix} 1 & 0 & 1 \end{bmatrix}

Explanation

\mathbf{s} = \begin{bmatrix} 1 & 1 & 1 \end{bmatrix}

Explanation

6. Consider the Meggitt decoder of

(7,4)

cyclic code generated by

\mathbf{g}(X) = 1 +X +X^3

. If the error location is

X^{3}

, then after how many shifts the error bit is corrected once the syndrome is formed in the syndrome register?

a: 4 Explanation

Explanation

b: 3 Explanation

Explanation

c: 2 Explanation

Explanation

d: 5 Explanation

Explanation

Cyclic codes