Digital Comparator Fundamentals

A magnitude comparator is a combinational circuit that compares two binary numbers in order to find out whether one binary number is equal, less than, or greater than the other binary number. We logically design a circuit for which we will have two inputs (A and B) and three output terminals: one for A > B condition, one for A = B condition, and one for A < B condition.

1-bit Comparator

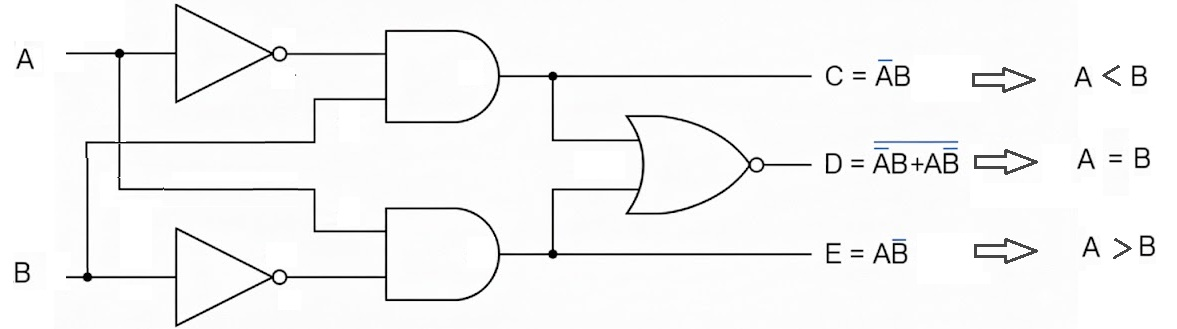
A 1-bit comparator compares two single-bit binary numbers A and B and produces three outputs: A > B, A = B, and A < B. Only one of these outputs will be high (1) at any given time, while the other two will be low (0).

Logic Equations

The outputs can be expressed as logical functions of input variables A and B as follows:

A > B = A · B' (A is 1 and B is 0)

A = B = A'B' + AB = A ⊙ B (Both A and B are same)

A < B = A' · B (A is 0 and B is 1)

Key Features

• Simple design using basic logic gates (AND, OR, NOT)
• Compares two 1-bit binary numbers
• Produces three mutually exclusive outputs
• Foundation for multi-bit comparator circuits
• Only one output is active at any time

Truth Table

A	B	A > B	A = B	A < B
0	0	0	1	0
0	1	0	0	1
1	0	1	0	0
1	1	0	1	0

Applications

• Basic building block for arithmetic circuits
• Decision-making circuits in digital systems
• Educational demonstrations of binary comparison
• Component in more complex comparator designs

2-bit Comparator

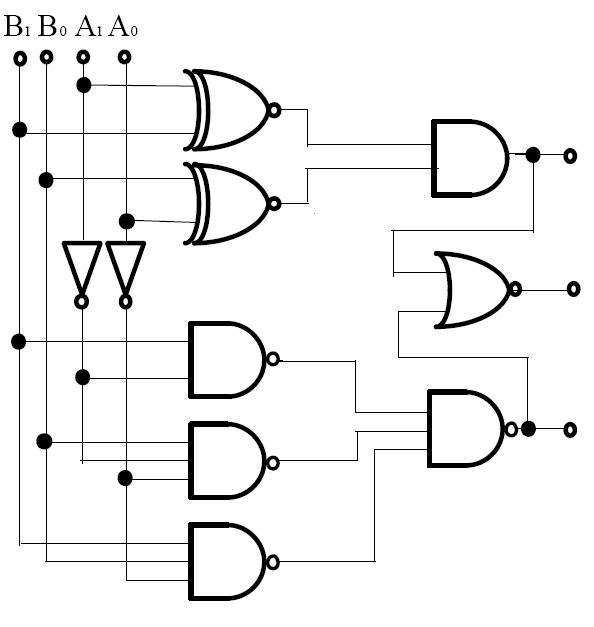
A 2-bit comparator compares two 2-bit binary numbers A₁A₀ and B₁B₀ and determines their relative magnitude. The comparison is performed by examining the most significant bits first, then the least significant bits if the MSBs are equal.

Comparison Algorithm

1. Compare MSBs first: If A₁ ≠ B₁, the result is determined by this comparison
2. If MSBs are equal: Compare the LSBs (A₀ and B₀) to determine the final result
3. Sequential priority: Higher-order bits have priority over lower-order bits

Logic Equations

A = B: Both numbers are equal when corresponding bits are equal

• (A = B) = (A₁ ⊙ B₁) · (A₀ ⊙ B₀)

A > B: A is greater when either:

• A₁ > B₁ (MSB of A is 1 and MSB of B is 0), OR
• MSBs are equal AND A₀ > B₀
• (A > B) = A₁B₁' + (A₁ ⊙ B₁) · A₀B₀'

A < B: A is less when either:

• A₁ < B₁ (MSB of A is 0 and MSB of B is 1), OR
• MSBs are equal AND A₀ < B₀
• (A < B) = A₁'B₁ + (A₁ ⊙ B₁) · A₀'B₀

Key Features

• Compares two 2-bit binary numbers (A₁A₀ and B₁B₀)
• Uses hierarchical comparison approach
• MSB comparison takes priority over LSB comparison
• Three mutually exclusive outputs
• Can be extended to larger bit widths

Truth Table

A₁	A₀	B₁	B₀	A < B	A = B	A > B
0	0	0	0	0	1	0
0	0	0	1	1	0	0
0	0	1	0	1	0	0
0	0	1	1	1	0	0
0	1	0	0	0	0	1
0	1	0	1	0	1	0
0	1	1	0	1	0	0
0	1	1	1	1	0	0
1	0	0	0	0	0	1
1	0	0	1	0	0	1
1	0	1	0	0	1	0
1	0	1	1	1	0	0
1	1	0	0	0	0	1
1	1	0	1	0	0	1
1	1	1	0	0	0	1
1	1	1	1	0	1	0

Applications

• Multi-bit arithmetic operations in digital systems
• Address comparison in memory systems
• Control logic in processors and microcontrollers
• Sorting and searching algorithms in hardware

2-bit Comparator Using Subtractor

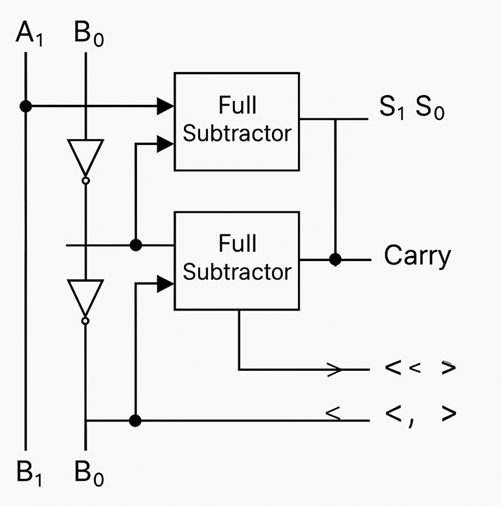
An alternative approach to implement a 2-bit comparator is to use a subtractor circuit. This method leverages the mathematical relationship between subtraction and comparison operations. When we subtract B from A (A - B), the result and associated flags can directly indicate the comparison relationship.

Principle of Operation

The subtractor-based comparator works on the principle that:

• If A - B > 0: Then A > B
• If A - B = 0: Then A = B
• If A - B < 0: Then A < B

Subtractor Circuit Analysis

A 2-bit subtractor performs the operation A₁A₀ - B₁B₀ using 2's complement arithmetic:

1. 2's Complement of B: First, find 2's complement of B₁B₀

   • 1's complement: B₁'B₀'
   • Add 1: B₁'B₀' + 1

2. Addition Process: Add A₁A₀ + (2's complement of B₁B₀)

3. Result Interpretation: Analyze the result to determine comparison

Implementation Using Full Adders

The subtractor can be built using full adders with the following connections:

For A₁A₀ - B₁B₀:

• Stage 0 (LSB):

  • Inputs: A₀, B₀' (inverted B₀), Cin = 1 (for 2's complement)
  • Outputs: S₀, C₀

• Stage 1 (MSB):

  • Inputs: A₁, B₁' (inverted B₁), Cin = C₀
  • Outputs: S₁, C₁

Comparison Logic from Subtractor Results

The comparison outputs can be derived from the subtractor results:

Equality (A = B):

• A = B when the subtraction result is zero
• (A = B) = S₁'S₀' (Both result bits are 0)

Greater Than (A > B):

• A > B when there is no borrow (positive result)
• (A > B) = C₁ (Carry out indicates no borrow)

Less Than (A < B):

• A < B when there is a borrow (negative result)
• (A < B) = C₁' (No carry out indicates borrow occurred)

Truth Table for Subtractor-Based Comparison

A₁	A₀	B₁	B₀	A-B (Decimal)	S₁	S₀	C₁	A>B	A=B	A<B
0	0	0	0	0	0	0	1	1	1	0
0	0	0	1	-1	1	1	0	0	0	1
0	0	1	0	-2	1	0	0	0	0	1
0	0	1	1	-3	0	1	0	0	0	1
0	1	0	0	1	0	1	1	1	0	0
0	1	0	1	0	0	0	1	1	1	0
0	1	1	0	-1	1	1	0	0	0	1
0	1	1	1	-2	1	0	0	0	0	1
1	0	0	0	2	1	0	1	1	0	0
1	0	0	1	1	0	1	1	1	0	0
1	0	1	0	0	0	0	1	1	1	0
1	0	1	1	-1	1	1	0	0	0	1
1	1	0	0	3	1	1	1	1	0	0
1	1	0	1	2	1	0	1	1	0	0
1	1	1	0	1	0	1	1	1	0	0
1	1	1	1	0	0	0	1	1	1	0

Advantages of Subtractor-Based Comparison

• Hardware Reuse: Can utilize existing adder/subtractor circuits
• Unified Arithmetic: Same circuit handles both arithmetic and comparison
• Efficient Design: Fewer dedicated logic gates for comparison function
• Scalable: Easily extended to larger bit widths

Disadvantages

• Complex Analysis: Requires understanding of 2's complement arithmetic
• Additional Logic: Need extra gates to interpret subtractor outputs
• Propagation Delay: Carry propagation through adder stages

Comparison Output Generation

From the subtractor results, the final comparison outputs are generated:

A = B = S₁' · S₀'           (Result is zero)
          A > B = C₁                  (No borrow occurred)
          A < B = C₁'                 (Borrow occurred)
          

Key Concepts for Students

1. 2's Complement Understanding: Essential for interpreting subtractor results
2. Borrow vs. Carry: Understanding the relationship between borrow and carry signals
3. Result Interpretation: How zero result indicates equality, positive indicates greater than
4. Circuit Connection: Proper connection of XOR gates for inversion and carry chain

This subtractor-based approach provides an alternative implementation method that demonstrates the close relationship between arithmetic operations and comparison functions in digital systems.

4-bit Comparator

A 4-bit comparator extends the comparison principle to handle 4-bit binary numbers A₃A₂A₁A₀ and B₃B₂B₁B₀. The comparison follows the same hierarchical approach, starting from the most significant bit.

Comparison Process

The comparison is performed by examining bits from MSB to LSB:

1. Compare A₃ and B₃: If different, this determines the result
2. If A₃ = B₃: Compare A₂ and B₂
3. If A₂ = B₂: Compare A₁ and B₁
4. If A₁ = B₁: Compare A₀ and B₀

Logic Equations

Equality Condition: The binary numbers A and B are equal if all corresponding bit pairs are equal:

x₃ = A₃ ⊙ B₃ = A₃'B₃' + A₃B₃ x₂ = A₂ ⊙ B₂ = A₂'B₂' + A₂B₂
x₁ = A₁ ⊙ B₁ = A₁'B₁' + A₁B₁ x₀ = A₀ ⊙ B₀ = A₀'B₀' + A₀B₀

(A = B) = x₃ · x₂ · x₁ · x₀

Greater Than Condition: A > B when A has a higher-order bit that is 1 while the corresponding bit of B is 0:

(A > B) = A₃B₃' + x₃A₂B₂' + x₃x₂A₁B₁' + x₃x₂x₁A₀B₀'

Less Than Condition: A < B when A has a higher-order bit that is 0 while the corresponding bit of B is 1:

(A < B) = A₃'B₃ + x₃A₂'B₂ + x₃x₂A₁'B₁ + x₃x₂x₁A₀'B₀

Key Features

• Handles 4-bit binary number comparison
• Hierarchical bit-by-bit comparison from MSB to LSB
• Efficient logic implementation using cascaded approach
• Foundation for even larger comparators
• Used in arithmetic logic units (ALUs) and processors

Implementation Strategy

• Bit-wise Equality: Each bit position generates an equality signal
• Priority Encoding: Higher-order differences override lower-order comparisons
• Cascaded Design: Can be built using smaller comparators
• Modular Approach: Easily expandable to n-bit comparators

Applications

• Arithmetic Logic Units (ALUs): Comparison operations in processors
• Memory Address Decoding: Range checking and address comparison
• Digital Signal Processing: Magnitude comparison in DSP algorithms
• Control Systems: Decision-making based on numerical comparisons
• Sorting Networks: Hardware-based sorting implementations