Virtual Labs

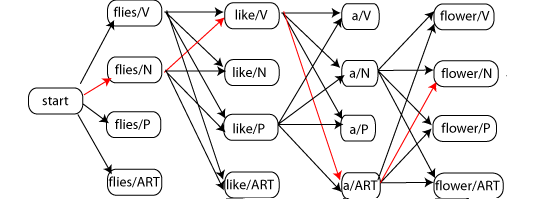
POS Tagging - Viterbi Decoding

Sequence decoding is a fundamental process in computational linguistics and Natural Language Processing (NLP) that involves finding the most probable sequence of hidden states (such as POS tags) given a sequence of observed words. The Viterbi algorithm is the standard dynamic programming solution for this task, especially when using Hidden Markov Models (HMMs).

What is Viterbi Decoding?

Viterbi decoding is the computational process of determining the most likely sequence of hidden states (tags) for a given sequence of observations (words), using:

Emission probabilities: Likelihood of a word given a tag
Transition probabilities: Likelihood of a tag following another tag
Initial probabilities: Likelihood of starting with a particular tag

The algorithm efficiently computes the optimal path through a trellis (table) using dynamic programming.

Core Components

1. Hidden Markov Model (HMM)

An HMM for POS tagging consists of:

Hidden States (Tags): e.g., Noun, Verb, Adjective, Determiner
Observations (Words): e.g., "the", "cat", "runs"
Transition Probabilities: P(tag₂ | tag₁)
Emission Probabilities: P(word | tag)
Initial Probabilities: P(tag₁)

2. The Decoding Problem

Given a sequence of words W = w₁, w₂, ..., wₙ and HMM parameters, find the most likely tag sequence T* = t₁, t₂, ..., tₙ:

$T^* = \arg\max_{T} P(T \mid W)$

Using the Markov and output independence assumptions, this becomes:

$T^* = \arg\max_{T} \prod_{i=1}^n P(w_i \mid t_i) \times P(t_i \mid t_{i-1})$

Viterbi Algorithm: Dynamic Programming Solution

Mathematical Foundation

For each word position j and tag s, we compute:

$V[s][j] = \max_{s'} \left( V[s'][j-1] \times a_{s',s} \right) \times b_s(w_j)$

Where:

V[s][j]: Maximum probability of any tag sequence ending in state s at position j
a_{s',s}: Transition probability from tag s' to tag s
b_s(w_j): Emission probability of word w_j given tag s

Algorithm Steps

1. Initialization (j = 1)

$V[s][1] = \pi[s] \times b_s(w_1)$

2. Recursion (j = 2 \ldots n)

For each state s:

$V[s][j] = \max_{s'} \left( V[s'][j-1] \times a_{s',s} \right) \times b_s(w_j)$

3. Termination

$P^* = \max_s V[s][n]$

$q^*_n = \arg\max_s V[s][n]$

4. Backtracking

For j = n-1 to 1:

$q^*_j = \text{Path}[q^*_{j+1}][j+1]$

Example Walkthrough

Sentence: "Book that flight"
Tags: {Noun, Verb, Det}

Emission Matrix P(word | tag):

	Book	that	flight
Noun	0.3	0.1	0.8
Verb	0.7	0.0	0.1
Det	0.0	0.9	0.0

Transition Matrix P(tag₂ | tag₁):

	Noun	Verb	Det
Noun	0.2	0.1	0.6
Verb	0.5	0.2	0.3
Det	0.8	0.2	0.0

Viterbi Table Computation:

Time t=1 (Book):
- V[Noun][1] = 0.33 × 0.3 = 0.10
- V[Verb][1] = 0.33 × 0.7 = 0.23
- V[Det][1] = 0.33 × 0.0 = 0.00
Time t=2 (that):
- V[Noun][2] = max(0.10×0.2, 0.23×0.5, 0.00×0.8) × 0.1 = 0.0115
- V[Verb][2] = max(0.10×0.1, 0.23×0.2, 0.00×0.2) × 0.0 = 0.0
- V[Det][2] = max(0.10×0.6, 0.23×0.3, 0.00×0.0) × 0.9 = 0.0621
Time t=3 (flight):
- V[Noun][3] = max(0.0115×0.2, 0.0×0.5, 0.0621×0.8) × 0.8 = 0.0398
- V[Verb][3] = max(0.0115×0.1, 0.0×0.2, 0.0621×0.2) × 0.1 = 0.0001
- V[Det][3] = max(0.0115×0.6, 0.0×0.3, 0.0621×0.0) × 0.0 = 0.0

Optimal Path: Verb → Det → Noun = "Book that flight"

Key Insights

Optimal Substructure: The best solution contains best solutions to subproblems.
Markov Property: Each tag depends only on the previous tag.
Probability Balance: The algorithm balances local (emission) and global (transition) probabilities.

Applications Beyond POS Tagging

Speech Recognition
Bioinformatics (gene/protein sequence analysis)
Named Entity Recognition
Machine Translation
Information Extraction

Practical Considerations

Smoothing: Handle unseen word-tag pairs (Laplace, Good-Turing, back-off).
Unknown Words: Use morphological analysis, character features, or embeddings.

Conclusion

The Viterbi algorithm is a cornerstone of sequence labeling in NLP, providing an efficient and mathematically sound method for decoding the most probable sequence of tags. This experiment lets you practice filling Viterbi tables and understanding dynamic programming in real-world POS tagging.