Types of Oscillators: Simple Harmonic, Damped and Forced.
Procedure for the experiment is as follows:
1.To study the Simple harmonic motion-
step1: Read the theory
-
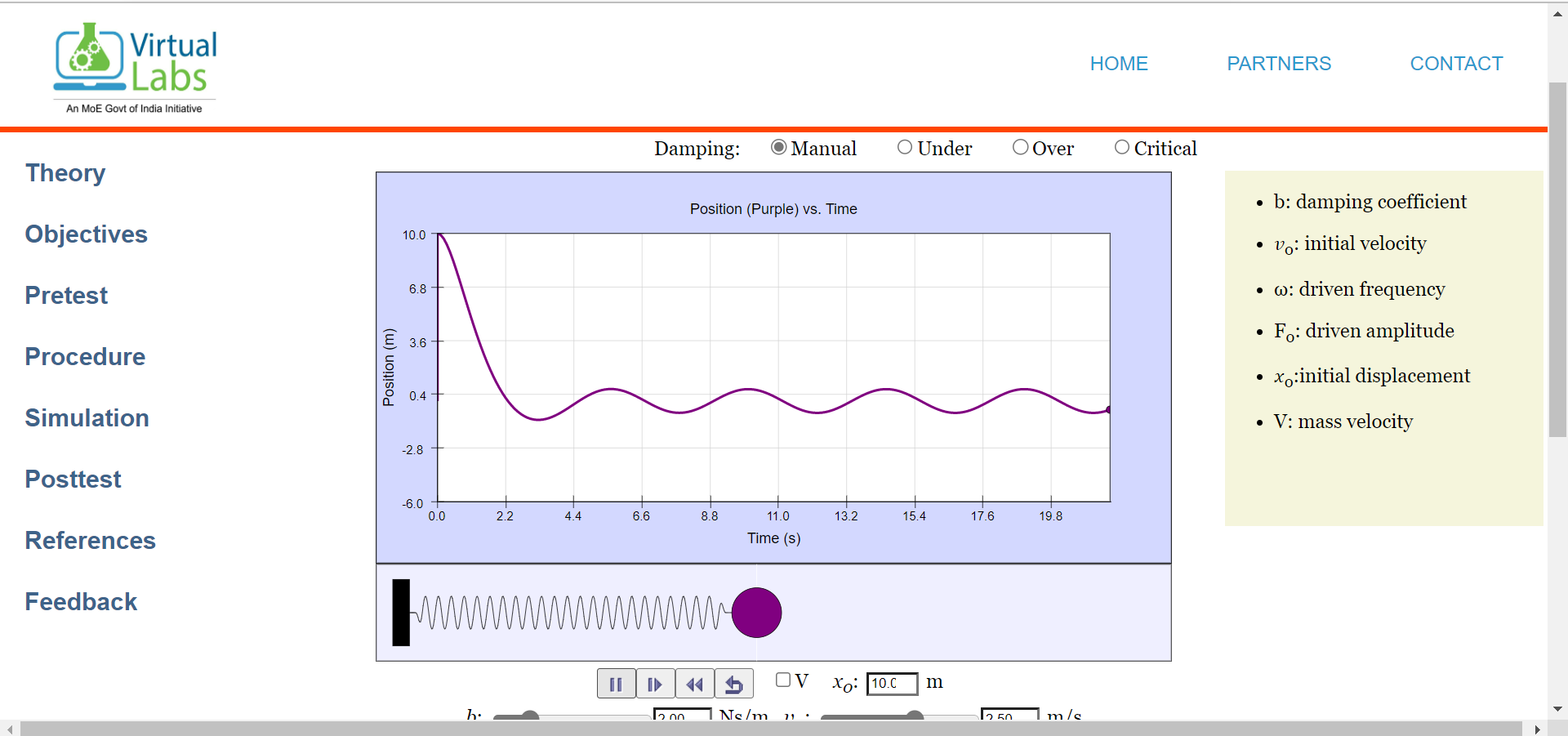
step2: Set the damping factor (b) = 0
-
step3: set vo= 0 m/s
-
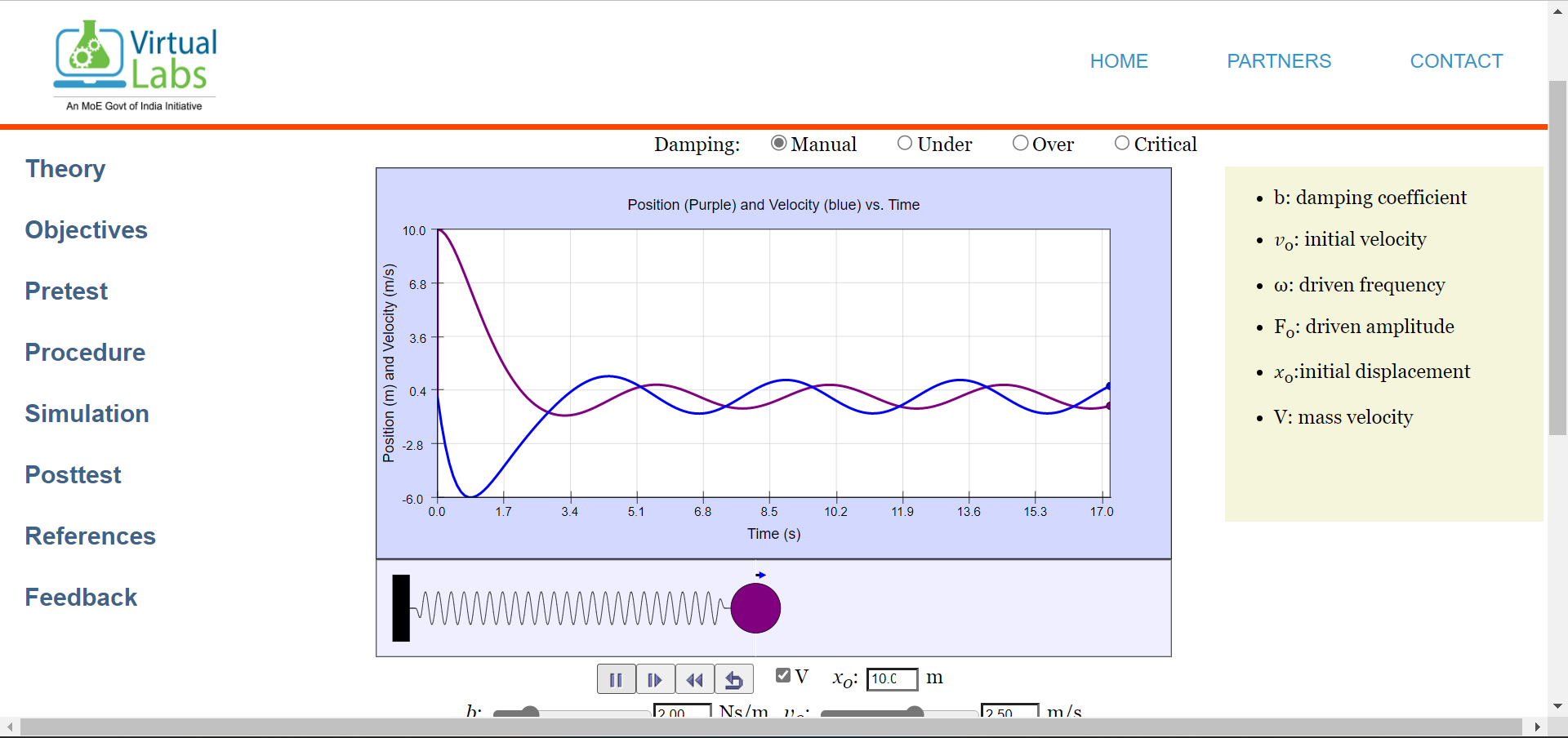
step4: Drag the ball to maximum starting position say xo= 10.0m and play the animation button.
-
step5: Observe the graph,wait until the animation ends
Graph representing S.H.M motion (position graph)
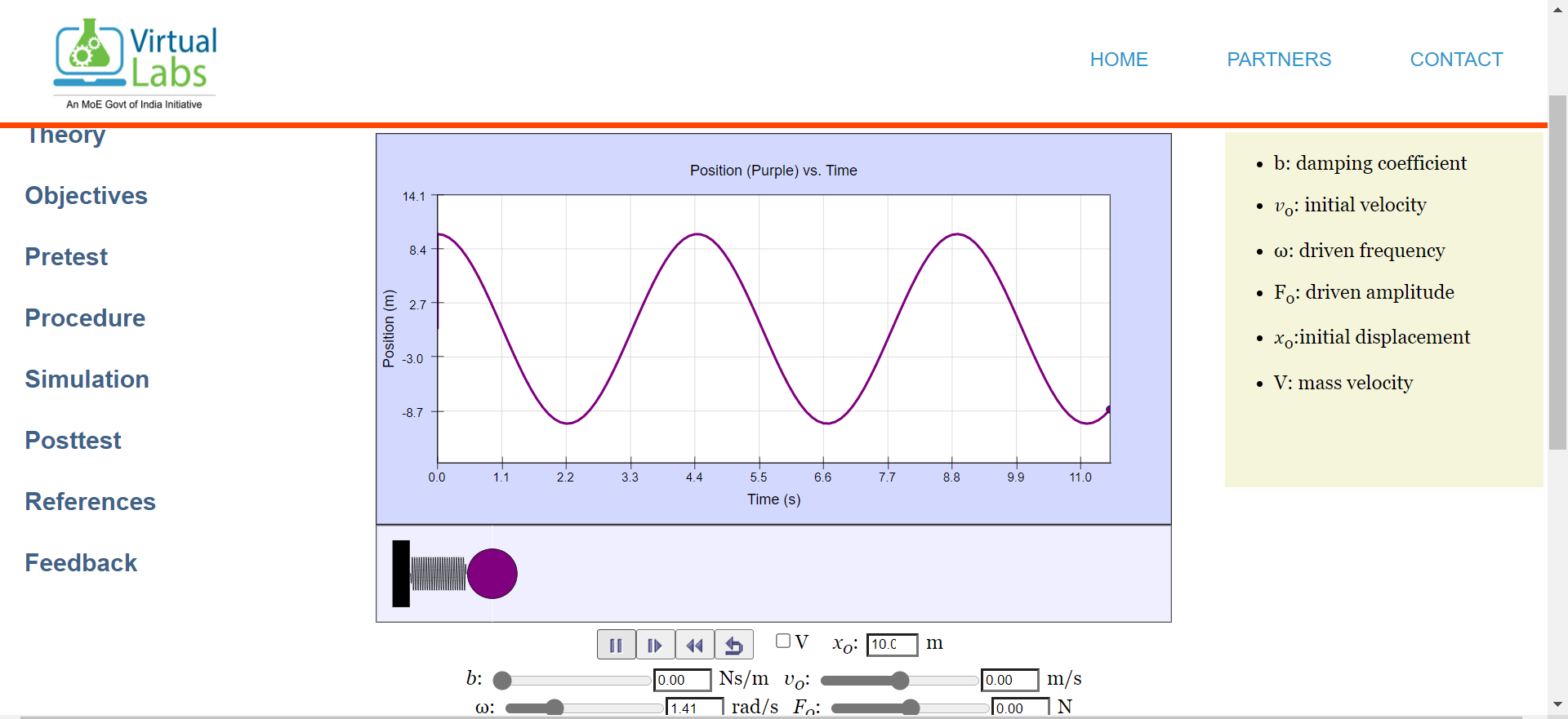
Graph representing S.H.M motion (position and velocity graph)
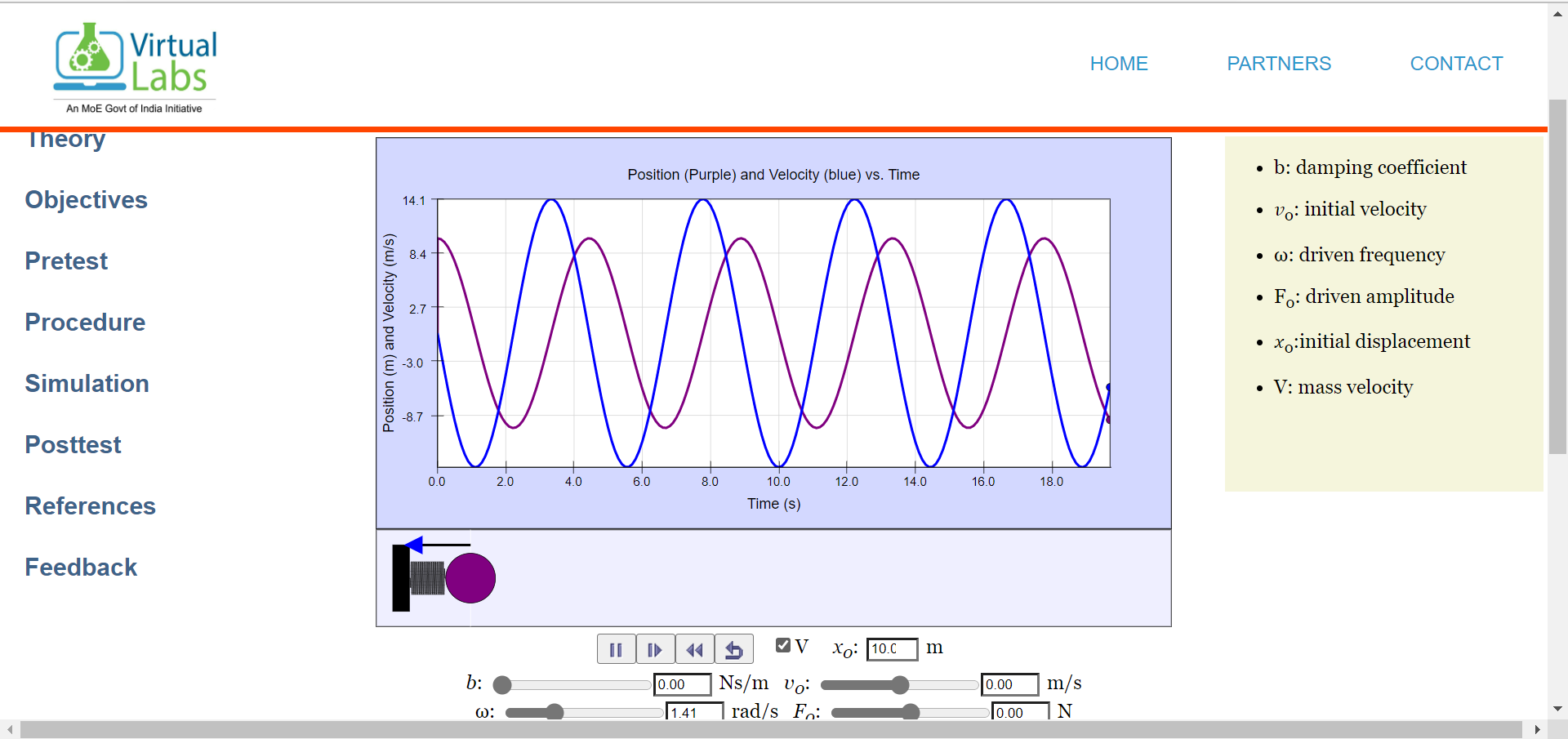
2.To study Damped oscillatory motion
step1: Reset the simulation
step2: Set vo= 0 m/sec
step3: change the damping factor(b) from 0 to some value take three cases and reset the simulation in each case
Case 1:Under-Damping
Case 2: Critical-Damping
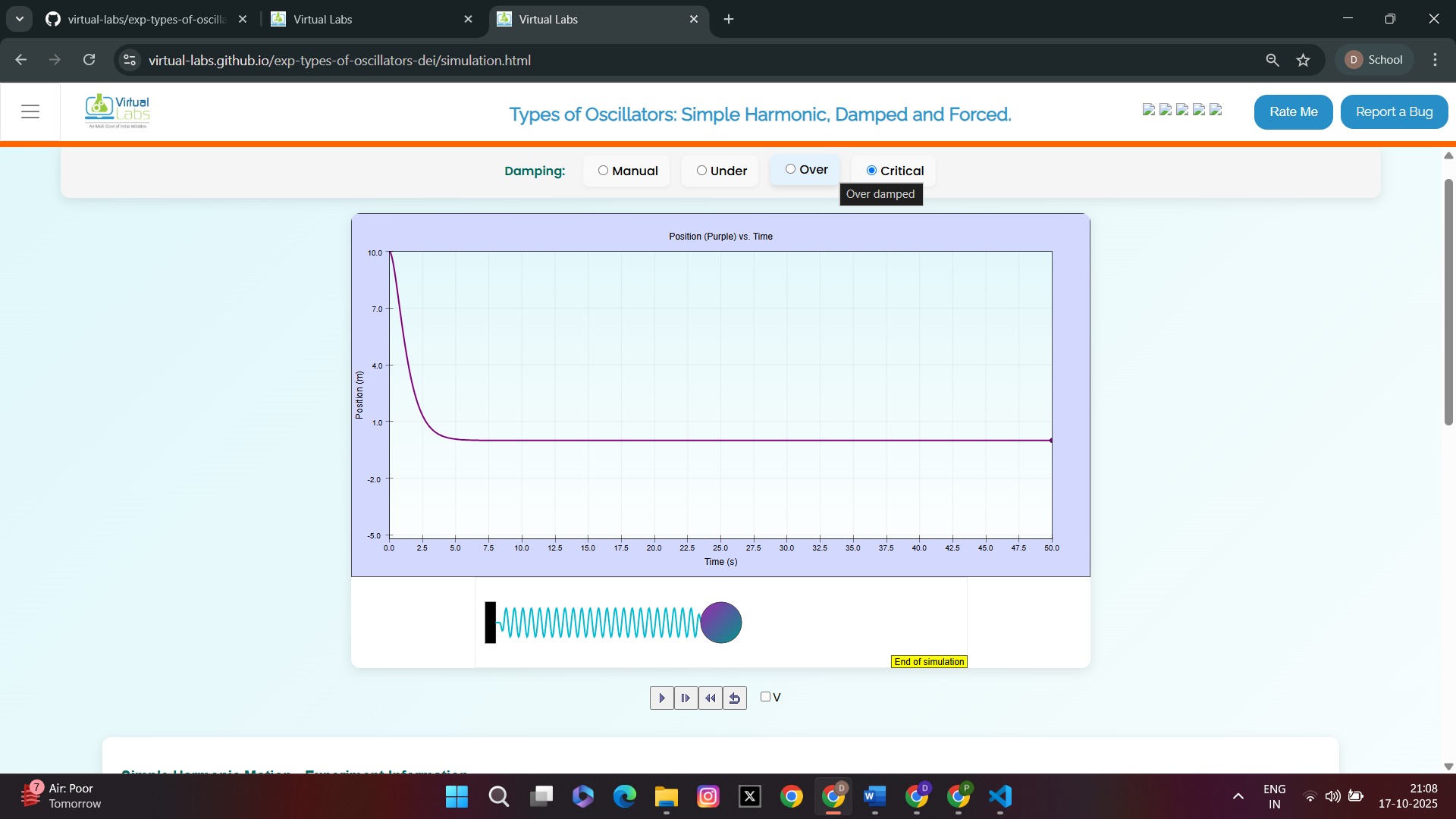
Case 3: Over-Damping
step4: Drag the ball to maximum starting position say xo= 10.0m and play the animation button.
step5: In all the above three cases mentioned observe the graph and wait till animation ends.
Set the value of b < 2√2 (say b= 0.5)
Graph representing under-damped oscillatory motion (position graph)
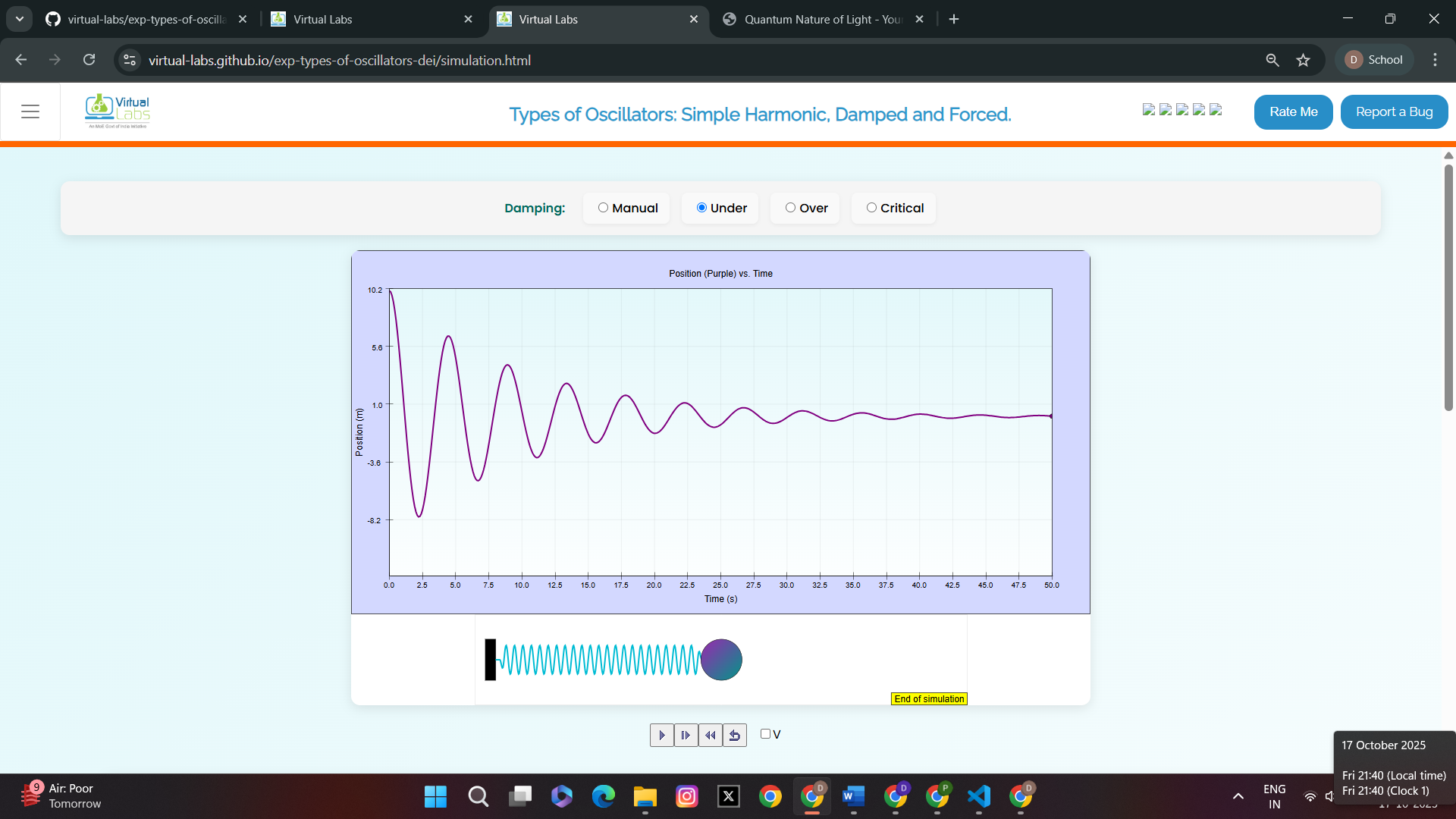
Graph representing under-damped oscillatory motion (position and velocity graph)
}})
Set the value of b = 2√2
Graph representing critical-damped oscillatory motion (position graph)
Graph representing critical-damped oscillatory motion (position and velocity graph)
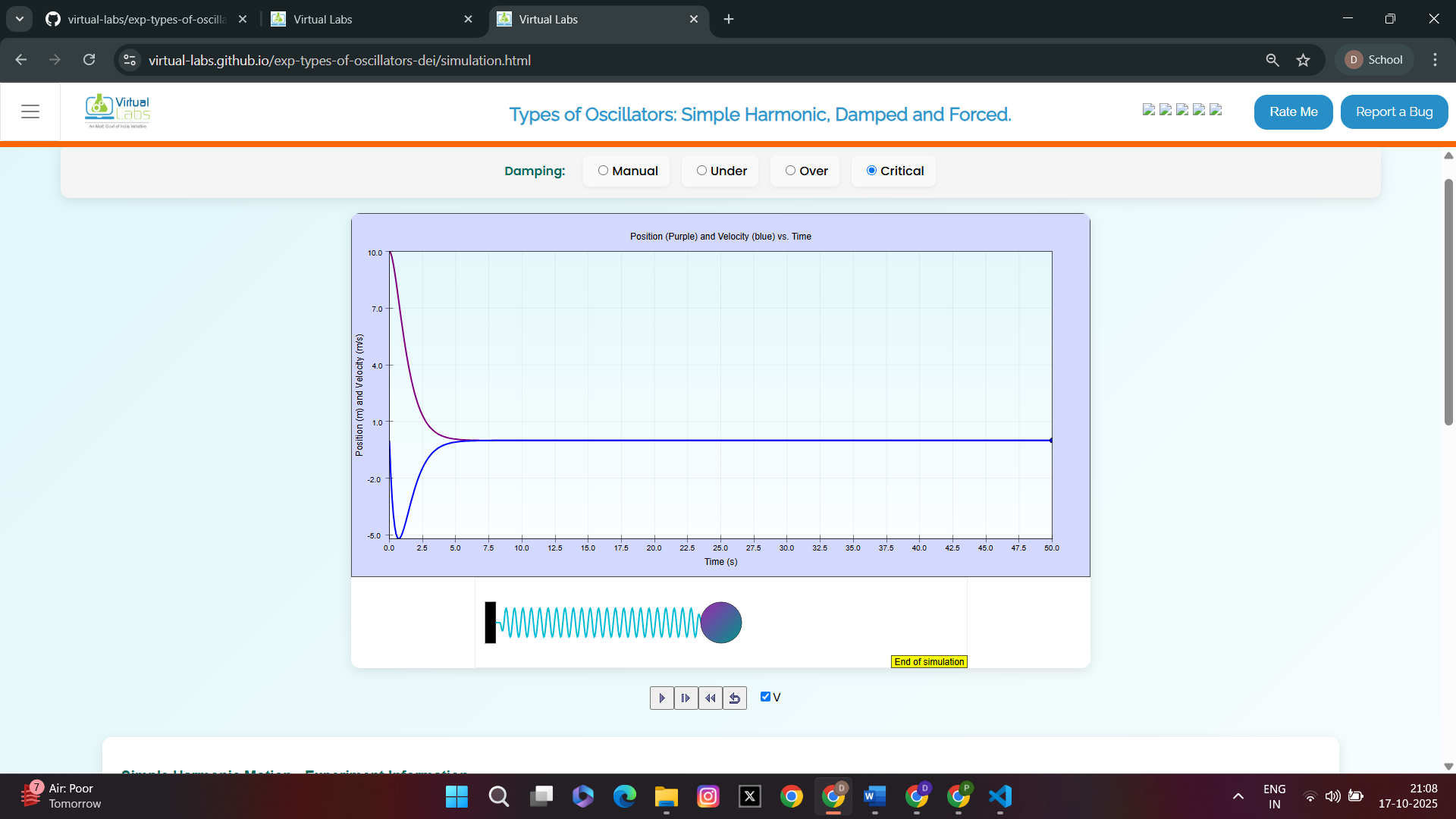
Set the value of b > 2√2 (say b= 3)
Graph representing over-damped oscillatory motion (position graph)
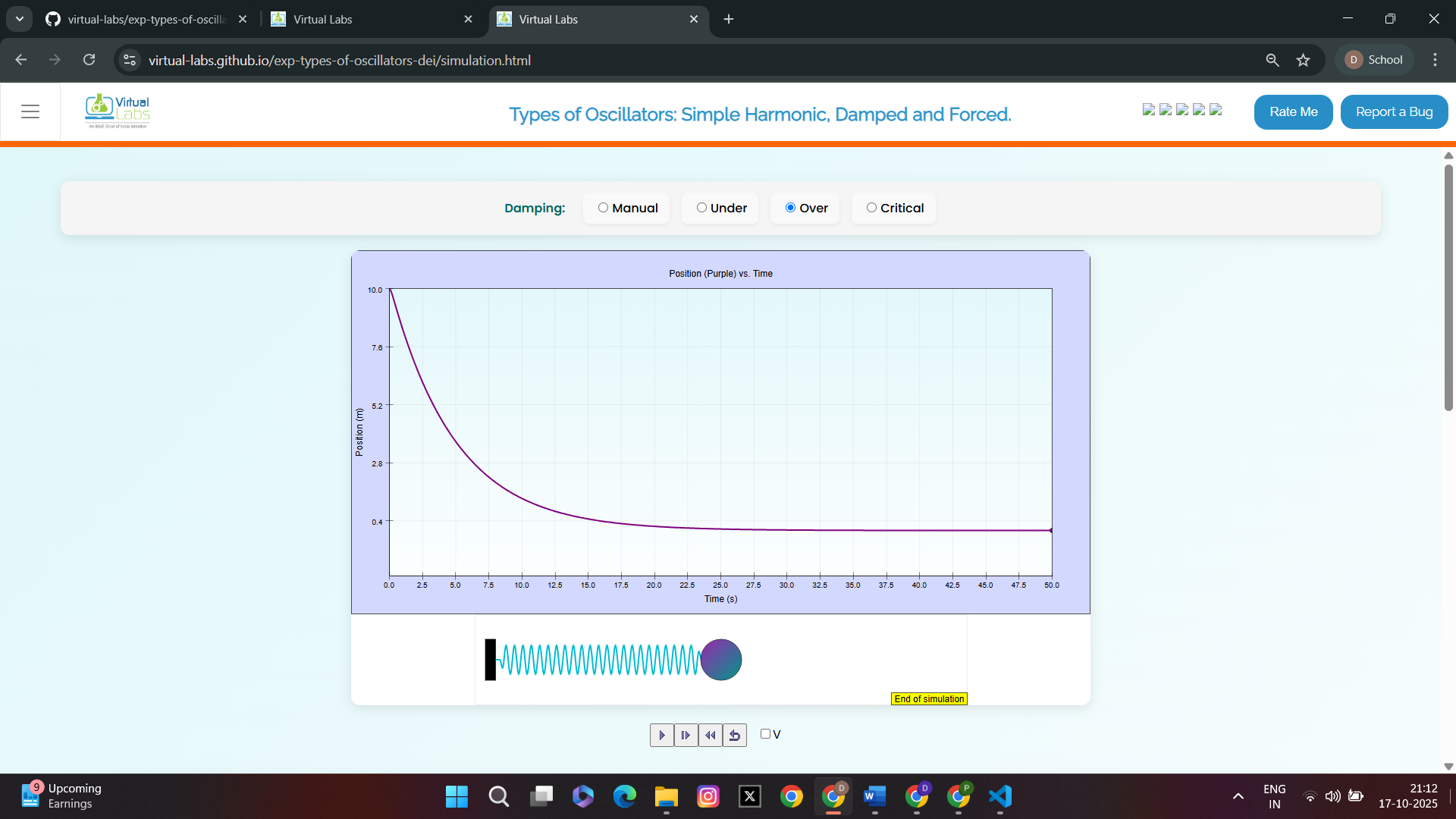
Graph representing over-damped oscillatory motion (position and velocity graph)
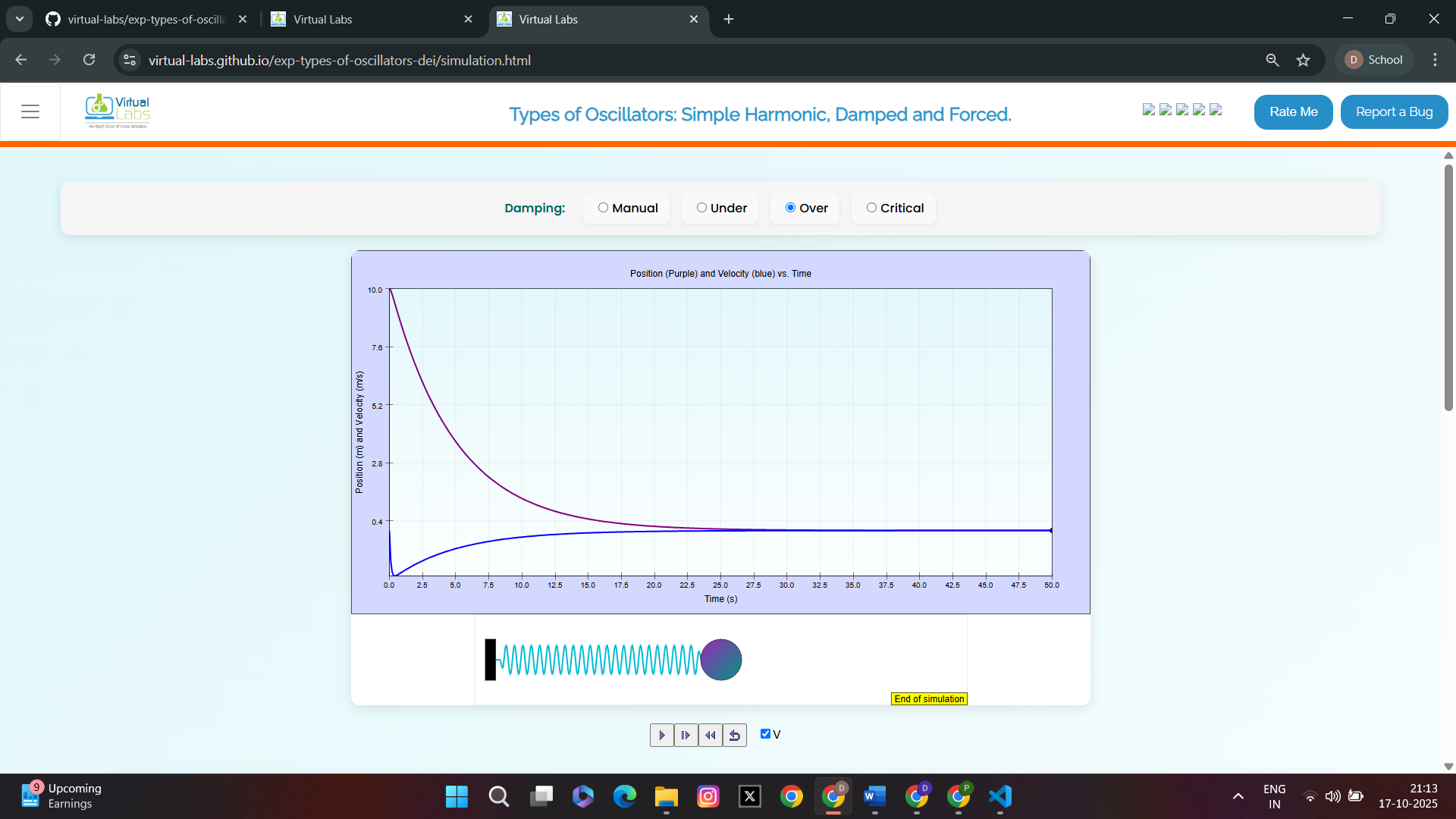
3.To study Forced oscillatory motion
-
step1: Reset the simulation again
-
step2: Set the damping coefficient (b) > 2√2
-
step3: Change the value of initial velocity vo= 2m/sec
-
step4: Set value of driven frequency(ω) = 1.41
-
step5: Set some value of driven amplitude Fo which will be the force for oscillation
-
step6: Drag the ball to maximum starting position say xo= 10.0m and play the animation button.
-
step7: Observe the graph till the animation ends
Graph representing forced-oscillatory motion (position graph)
Graph representing forced-oscillatory motion (position and velocity graph)
Perform the following experiments
Experiment-1:
Perform experiment to calculate the value of k (spring constant) in the following cases described below.In each case record observations into the table and compute the value of k.Take value of m =1 kg in each case.
Case 1: Free oscillator (simple harmonic motion) when b = 0
set different values for xo
keep other parameters = 0
record the value of time in each case
calculate corrosponding angular frequency
then compute k (spring constant) using formula
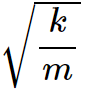
Computed value of k:__________
Case 2:Under-Damped damped Oscillator when b < 2√2
set different values for xo
set b<2√2 and keep other parameters = 0
record the value of time in each case
calculate corrosponding angular frequency:
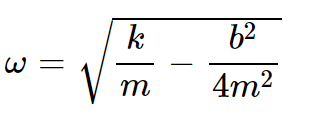
Value of b used in the experiment:_________
| S.no | xo (displacement) | f (frequency) | ω (angular frequency) |
|---|---|---|---|
| 1. | |||
| 2. | |||
| 3. | |||
| 4. | |||
| 5. | |||
| 6. |
The mean ω: _________
| S.no | xo (displacement) | f (frequency) | ω (angular frequency) |
|---|---|---|---|
| 1. | |||
| 2. | |||
| 3. | |||
| 4. | |||
| 5. | |||
| 6. |
The mean = ________
computed value of k=_____________
Case 3: Forced oscillator when b > 2√2
set different values for Fo
set driven frequency ω =1rad/sec,
obtain the value of amplitude by observing graph each time.
obtain the value of ω using the relation:
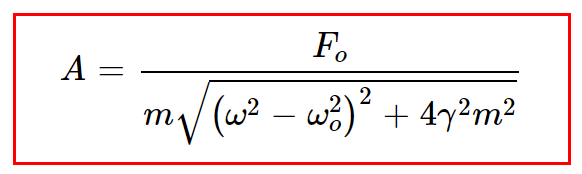
then compute k (spring constant) from the calculated mean value of
The mean ω = ________
computed value of k =_____________
| S.no | Fo (force) | A (amplitude) | ω (angular frequency) |
|---|---|---|---|
| 1. | |||
| 2. | |||
| 3. | |||
| 4. | |||
| 5. | |||
| 6. |
