Tools

Tuned Dynamic Vibration Absorber

A vibration absorber is a mechanical device which is tuned to reduce or eliminate undesired vibrations, it must shift the natural frequencies, away from the excitation frequency, as shown in Fig. 1.

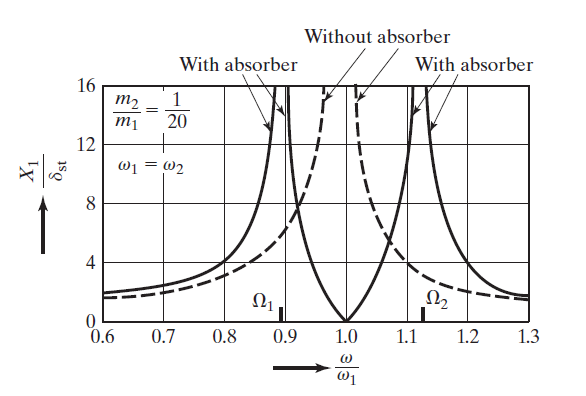
Alt text
Fig. 1 Comparing response of system, with and without absorber

An additional spring mass system is attached to the main spring mass system, so that the resonance of the original system will not occur. The addition of spring mass system results in a two degree of freedom system, having two natural frequencies. General applications include reciprocating tools such as saws, drills, rotary hammers which requires to balance the reciprocating force. Fig. 2 shows a schematic representation of an undamped dynamic vibration absorber.

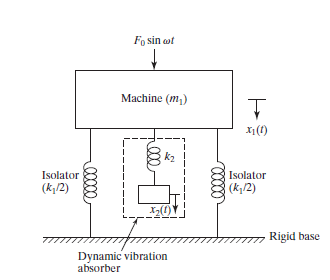
Alt text

Fig. 2 Undamped dynamic vibration absorber.

Mathematically, a mass m2m_2 attached to a machine of mass m1m_1, through a stiffness of k2k_2, will be

m1x¨1+k1x1+k2(x1−x2)=F0sin⁡ωtm_1 \ddot{x}_1 + k_1 x_1 + k_2 (x_1 - x_2) = F_0 \sin \omega t
m2x¨2+k2(x2−x1)=0m_2 \ddot{x}_2 + k_2 (x_2 - x_1) = 0

By assuming harmonic solution,

xj(t)=Xjsin⁡ωt,j=1,2x_j(t) = X_j \sin \omega t, \quad j = 1, 2

The steady state amplitudes are,

X1=(k2−m2ω2)F0(k1+k2−m1ω2)(k2−m2ω2)−k22X_1 = \frac{(k_2 - m_2 \omega^2) F_0}{(k_1 + k_2 - m_1 \omega^2)(k_2 - m_2 \omega^2) - k_2^2}
X2=k2F0(k1+k2−m1ω2)(k2−m2ω2)−k22X_2 = \frac{k_2 F_0}{(k_1 + k_2 - m_1 \omega^2)(k_2 - m_2 \omega^2) - k_2^2}

To reduce amplitude of m1m_1, X1X_1 is substituted as zero, leading to

ω2=k2m2\omega^2 = \frac{k_2}{m_2}

The absorber is designed such that the amplitude of vibration of the machine, while operating at its original resonant frequency, will be zero.
By defining,

δst=F0k1\delta_{st} = \frac{F_0}{k_1}

and the natural frequency of m1 and m2 as ω1 and ω2 ,

ω1=(k1m1)1/2\omega_1 = \left( \frac{k_1}{m_1} \right)^{1/2} ω2=(k2m2)1/2\omega_2 = \left( \frac{k_2}{m_2} \right)^{1/2}

The steady state amplitudes can be written as,

X1δst=1−(ωω2)2[1+k2k1−(ωω1)2][1−(ωω2)2]−k2k1\frac{X_1}{\delta_{st}} = \frac{1 - \left( \frac{\omega}{\omega_2} \right)^2}{\left[ 1 + \frac{k_2}{k_1} - \left( \frac{\omega}{\omega_1} \right)^2 \right] \left[ 1 - \left( \frac{\omega}{\omega_2} \right)^2 \right] - \frac{k_2}{k_1}}
X2δst=1[1+k2k1−(ωω1)2][1−(ωω2)2]−k2k1\frac{X_2}{\delta_{st}} = \frac{1}{\left[ 1 + \frac{k_2}{k_1} - \left( \frac{\omega}{\omega_1} \right)^2 \right] \left[ 1 - \left( \frac{\omega}{\omega_2} \right)^2 \right] - \frac{k_2}{k_1}}

At ω=ω1\omega=\omega_1 substituting X1=0X_1 = 0, which gives,

X2=−k1k2δst=−F0k2X_2 = -\frac{k_1}{k_2} \delta_{st} = -\frac{F_0}{k_2}

This shows that the force exerted by the auxiliary spring is opposite to the impressed force, neutralizing it, thus reducing X1X_1 to zero.