Scaling in 3D space is a fundamental geometric transformation that involves resizing objects by multiplying their coordinates with constant factors along each axis. This transformation preserves the shape of objects when applied uniformly, but can distort them when applied non-uniformly.

The scaling transformation is represented by a scaling matrix, denoted as S_v, where v represents the scaling factors. The matrix scales points by factors v_x, v_y, and v_z along the X, Y, and Z axes respectively.

The scaling matrix in 3D:

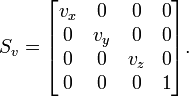
Given a vector [x, y, z], after applying the scaling transformation:

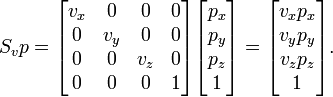
A scaling transformation can be interpreted in two ways:

1. As resizing the coordinate axes while keeping the points constant. For example, a scaling by (2, 3, 4) would require redrawing each unit on the X-axis as 2 units, each unit on the Y-axis as 3 units, and each unit on the Z-axis as 4 units.
2. As moving points away from or towards the origin by multiplying their coordinates with the scaling factors.

There are two types of scaling transformations:

1. Uniform Scaling: When v_x = v_y = v_z, the object maintains its shape while being enlarged or reduced proportionally in all directions. For example, scaling by (2, 2, 2) doubles the size of the object while preserving its proportions.
2. Non-uniform Scaling: When the scaling factors differ (v_x ≠ v_y ≠ v_z), the object is stretched or compressed differently along each axis, potentially distorting its shape. For instance, scaling by (2, 1, 3) would stretch the object twice as much along the X-axis, leave it unchanged along the Y-axis, and stretch it three times along the Z-axis.

This fundamental concept is integral to understanding how objects can be enlarged, reduced, or distorted in 3D space through scaling transformations, and is widely used in computer graphics, 3D modeling, and animation.