All the electrical equipment and machines work on supplying electric power and dissipating large amounts of energy. The supplied power is usually measured in terms of watts using a device namely a wattmeter. A wattmeter is also called a deflection meter which is mainly used in electrical labs. It not only measures power in terms of watts but also measures in terms of Kilowatts and Megawatts. The wattmeter usually consists of two coils "CC" current coil which is usually connected in series with load current and a voltage/pressure/ potential coil "PC", this coil is usually connected across the load circuit. Electrical power can be represented in three forms they are Active power, Reactive power and Apparent power. The following theory describes the two-wattmeter method at a balanced load condition.

What is The Wattmeter Method?

Three-phase two-wattmeter measures the current and voltage from any of the 2 supply lines of 3 phases corresponding to the 3rd supply line of 3 phases. The 3-phase two-wattmeter is said to be at a balanced load condition if the current in every phase lags at an angle "φ" with phase voltage.

Construction of Two Wattmeter Method

The 3-phase power of a 3-phase circuit can be measured using three ways:

• Three Wattmeter Method
• Two Wattmeter Method
• One Wattmeter Method
  

The main concept of two two-wattmeter with 3 phase voltage is to balance the 3 phase load by satisfying the condition of current lagging at an angle ‘φ’ with the phase voltage. The circuit diagram of 3 phase two wattmeter is shown below:

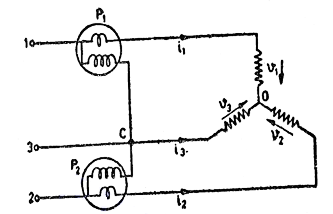
Fig. 1 Three-phase power measurement using Two Wattmeter

It consists of two Wattmeters like P₁ and P₂, Where each wattmeter has a current coil ‘CC’ and a pressure coil ‘PC’. Here, One end of wattmeter P₁ is connected to the ‘1’ terminal whereas one end of wattmeter P₂ is connected to the ‘2’ terminal. The circuit also consists of 3 resistors which are constructed in a star topology. The two ends of resistors are connected to 2nd terminals of a wattmeter whereas the third terminal of the resistor is connected to 3.

Derivation of Two Wattmeter Method

Two Wattmeter is used to determine two main parameters they are,

• Active Power
• Power factor
  

Consider the load used as a resistive load which is represented by following the phasor diagram as shown below.

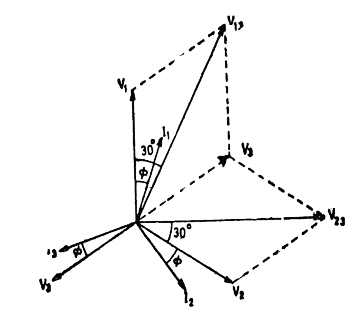
Fig 2. Phasor diagram for balanced Star Connected Load

Instantaneous power consumed by load = v₁i₁ + v₂i₂ + v₃i₃

Let us consider two wattmeters connected to measure power in three-phase circuits as shown in Fig. 1 Star connection.

Instantaneous reading of P₁ wattmeter p₁ = i₁ (v₁-v₃).

Instantaneous reading of P₂ wattmeter p₂ = i₂ (v₂-v₃).

Sum of Instantaneous readings of two wattmeters = p₁ + p₂

$$=i_1 (v_1-v_3) + i_2 (v_2-v_3) = v_1i_1 + v_2i_2 - v_3 (i_1+i_2)$$

From Kirchhoff's law,

$$i_1 + i_2 + i_3 = 0$$

$$i_3 = -(i_1+i_2)$$

Therefore, Sum of Instantaneous readings of two wattmeters = v₁i₁ + v₂i₂ + v₃i₃

Therefore, The sum of the two-wattmeter reading is equal to the power consumed by the load. This is irrespective of whether the load is balanced or unbalanced.

Let V₁, V₂, V₃ be the rms values of phase voltage and I₁, I₂, I₃ be the rms values of phase currents.

The load is balanced, therefore

Phase voltages V₁ = V₂ = V₃ = V (say)

Line voltages V₁₃ = V₂₃ = V₁₂ = √3V

Phase currents I₁ = I₂ = I₃ = I (say)

Line currents I₁ = I₂ = I₃ = I

Power factor = cosφ

The phase currents lag the corresponding phasor voltages by an angle φ.

The current through wattmeter P₁ is I₁ and the voltage across its pressure coil is V₁₃. I₁ leads V₁₃ by an angle (30° - φ).

Therefore, Reading of P₁ wattmeter,

$$P_1 = V_{13}I_1cos(30° - φ) = √3VIcos(30° - φ)$$

The current through wattmeter P₂ is I₂ and voltage across its pressure coil is V₂₃. I₂ lags V₂₃ by an angle (30° + φ).

Therefore, Reading of P₂ wattmeter,

$$P_2 = V_{23}I_2cos(30° + φ) = √3VIcos(30° + φ).$$

A sum of reading of two wattmeters,

$$P_1 + P_2= √3VI[cos(30° - φ) + cos(30° + φ)] = 3VIcosφ$$

This is the total power consumed by the load.

Therefore, Total power consumed by load P = P₁ + P₂

Difference of readings of two wattmeters

$$P_1-P_2 = √3VI[cos(30° - φ) - cos(30° + φ)] = √3VIsinφ$$

$$\frac{P1-P2}{P1+P2} = \frac{√3VIsinφ}{3VIcosφ} = \frac{tanφ}{√3}$$

$$φ = tan^{-1}√3\frac{P1-P2}{P1+P2}$$

Power factor,

$$cosφ = cos \left (tan^{-1}√3\frac{P1-P2}{P1+P2} \right )$$

Advantages of Two Wattmeter Method:

• Both balanced and unbalanced loads can be balanced using this method.
• In a star-connected load, it is optional to connect the neutral point and wattmeter.
• In a delta, connected load connections need not be opened to connect the wattmeter.
• 3-phase power can be measured using two two-wattmeter.
• Both power and power factor are determined on a balanced load condition.

Disadvantages of Two Wattmeter Method:

• Not suitable for 3-phase, 4-wire system.
• Primary windings P₁ and secondary windings P₂ must be identified correctly to prevent incorrect results.

Applications of Two Wattmeter

• Wattmeters are used to measure the power consumption of any electrical appliances.