Thevenin's Theorem and the Superposition Theorem are fundamental tools in linear electrical circuit analysis.

1. Thevenin's Theorem : Thevenin's theorem provides a method to simplify any complex linear circuit into a very simple equivalent circuit.

Statement:
• Any two-terminal, linear electrical network containing voltage sources, current sources, and resistors can be replaced by an equivalent circuit consisting of a single voltage source (Thevenin Voltage) in series with a single resistor (Thevenin Resistance).
• (Thevenin Voltage) is the open-circuit voltage measured across the two terminals.
• (Thevenin Resistance) is the equivalent resistance measured across the two terminals when all independent sources are turned off(i.e., independent voltage sources are replaced by short circuits, and independent current sources are replaced by open circuits).
• This equivalent circuit, known as the Thevenin equivalent circuit, is particularly useful when you need to analyze the behavior of the circuit across a changing load connected to the two terminals.
The circuit diagram shown below consists of a network connected to a load resistor R_L.

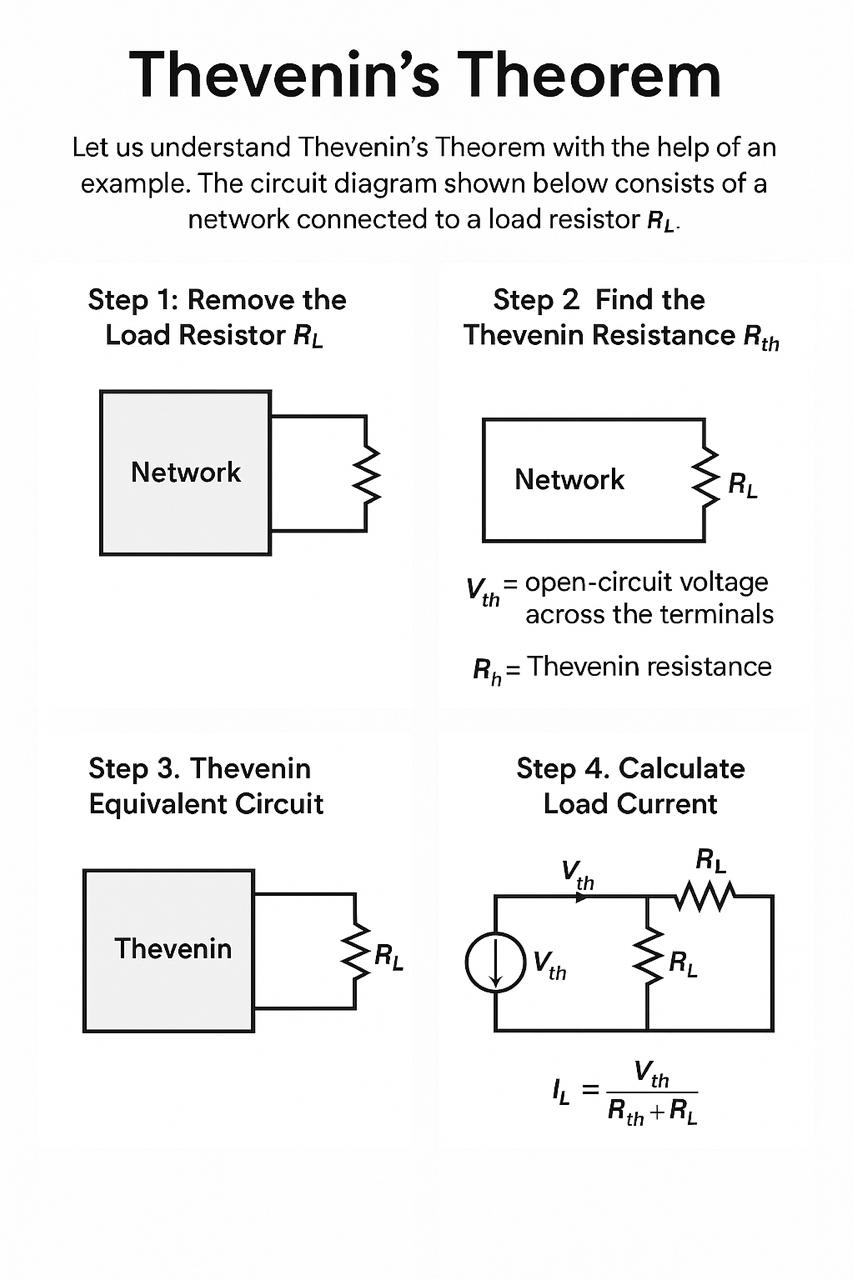
Step 1: Remove the Load Resistor R_L
The open-circuit voltage across these terminals is known as V_th, calculated using standard circuit analysis techniques.

Step 2: Find the Thevenin Resistance R_th
Now deactivate all independent sources :
• Replace voltage sources with a short circuit.
• Replace current sources with an open circuit.
• Then, calculate the equivalent resistance across the open terminals. This resistance is called R_th.

Step 3: Thevenin Equivalent Circuit
Now construct the Thevenin equivalent circuit using the calculated values of V_th and R_th. Connect the load resistor R_L back to this simplified circuit.

Step 4: Calculate Load Current
The load current I_L flowing through R_L can be calculated using Ohm’s Law:
Where:
V_th = Thevenin Voltage
R_th = Thevenin Resistance
R_L = Load Resistance

Conclusion:
Thevenin’s Theorem allows you to simplify a complex circuit into a simple two-component equivalent, making analysis easier—especially when studying the effect of varying the load resistor R_L.

2. Superposition Theorem : The Superposition Theorem is used to analyze linear circuits that contain multiple independent sources (voltage or current sources).

Statement:
• In any linear, bilateral network having more than one independent source, the current through or voltage across any element is the algebraic sum of the responses (currents or voltages) produced by each independent source acting alone, while all other independent sources are replaced by their internal resistances.

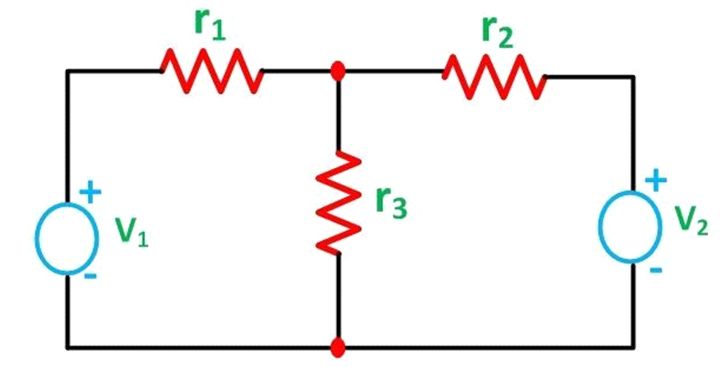
Let us understand the superposition theorem with the help of an example. The circuit diagram is shown below consists of two voltage sources V₁ and V₂.

First, take the source V₁ alone and short circuit the V₂ source as shown in the circuit diagram below:

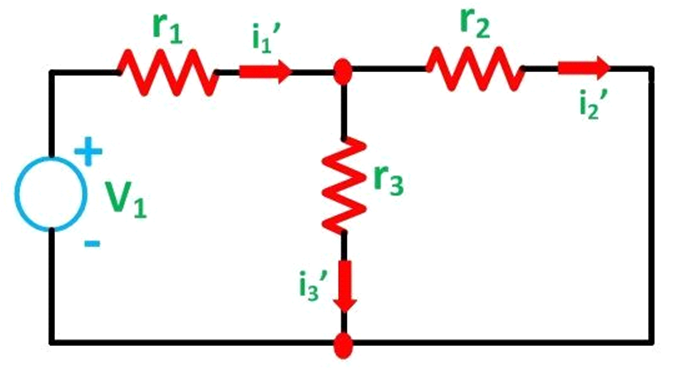
Here, the value of current flowing in each branch, i.e. i₁', i₂' and i₃' is calculated by the following equations.

The difference between the above two equations gives the value of the current i₃'.

i₃′ = i₁′ − i₂′......(3)

Now, activating the voltage source V₂ and deactivating the voltage source V₁ by short-circuiting it, find the various currents, i.e. i₁'', i₂'', i₃'' flowing in the circuit diagram shown below

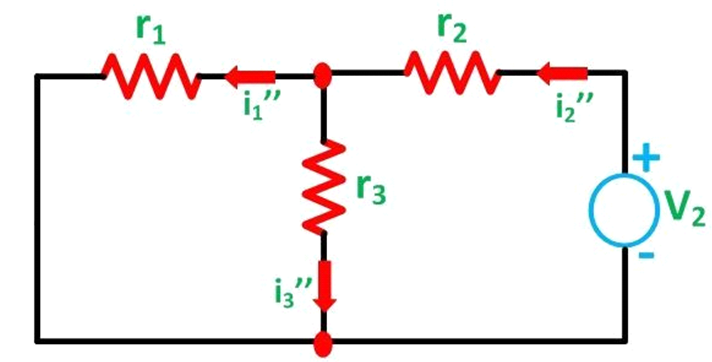
Here,

i₂″ = V₂ / [(r₁·r₃) / (r₁ + r₃) + r₂] ———(4)

and

i₁″ = i₂″ · (r₃ / (r₁ + r₃))———-(5)

And the value of the current i₃'' will be calculated by the equation shown below:

i₃″ = i₂″ − i₁″———(6)

As per the superposition theorem, the value of current i1, i2, i3 is now calculated as:

i₃ = i₃′ + i₃″ ——(7)

i₂ = i₂′ − i₂″——(8)

i₁ = i₁′ − i₁″———(9)

The direction of the current should be taken care of while finding the current in the various branches.