Theory

Audio signals generated by many musical instruments can be approximately expressed as combination of multiple sinusoids of appropriate frequencies and amplitudes. Thus, musical notes can be synthesized by combining a bunch of sinusoids. In this experiment we will digitally synthesize signals and listen to them. An example of a musical note is the sound generated by pressing a key of the piano.

Pure tone signal

A single frequency continuous-time sinusoid of frequency $f_0$ is given by

$$\text{x}(t) = a \sin(2 \pi f_0 t)$$

Since a computer can only generate sampled signals, let us fix a sampling rate of $F_s$ samples per second. A digital recording device samples an audio signal at a certain sampling rate (given by the device specifications). In a similar manner, a digital playback device converts the sampled audio signal into a continuous-time signal following the specified sampling rate. The choice of sampling rate depends on the largest frequency content of the signal and is given by the Nyquist sampling criterion. Specifically, to sample a signal with highest frequency of $f_0$, the sampling rate should be chosen as $F_s >= 2 f_0$. This will allow for exact reconstruction of the signal without any loss of information. The sampled signal is given by $$\text{x}[n] = a \sin(2 \pi f_0 n T_s)$$

where $T_s = \frac{1}{F_s}$ is the sampling interval. A signal of only one frequency is called a pure tone signal. We will synthesise a single tone signal and listen to its sound for various choices of $F_s$ and $f_0$.

Aliasing

Aliasing is a peculiar phenomenon, happens when the sampling rate does not obey Nyquist sampling criteria. Due to lack of sufficient samples, the high frequencies show up as lower frequencies. For example, let $F_s = 8000$ Hz and let a pure tone of frequency $f_0 = 6000$ Hz is to be synthesised. On applying the above formula, the signal is

$$\text{x}[n] = a \sin(2 \pi f_0 n T_s) = a \sin(2 \pi (F_s-f_0) n T_s)$$

Thus, a signal of frequency $f_0 = 6000$ Hz is not distinguishable from a signal of frequency $f_s-f_0 = 2000$ Hz. To avoid aliasing, given a sampling frequency of $F_s$, frequencies less than $\frac{F_s}{2}$ should only be synthesized.

Envelope

Most audio signals from musical instrument will have a characteristic amplitude envelope corresponding to gradual rise and fall of the volume at beginning and end of a note. Thus, while artificially synthesizing music signals, an envelope is applied. This makes the audio signal sound natural. One such example is the attack-decay-sustain-release (ADSR) envelope. An example figure is shown below:

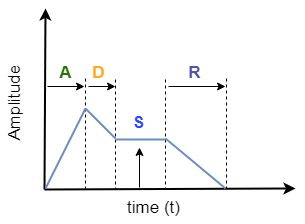
Another example is the exponential decay envelop shown in figure below:

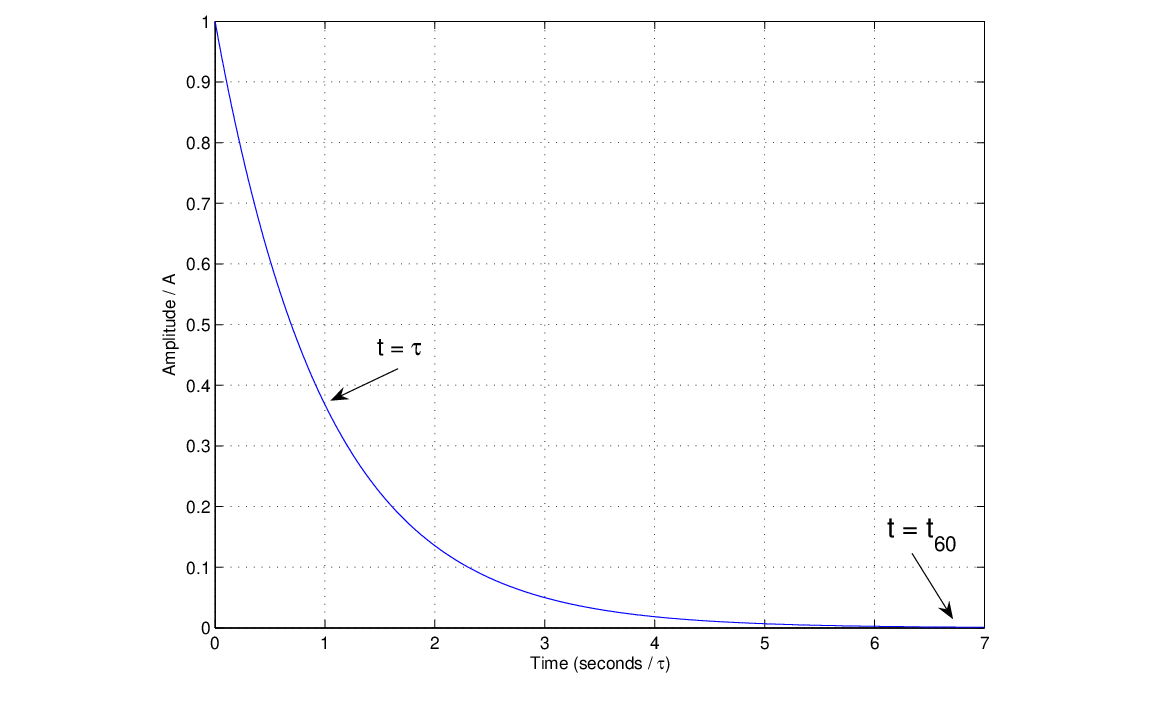
Harmonics

Signals with frequencies $2f_0$, $3f_0$, etc. are called harmonics of the frequency $f_0$, i.e., their frequency is an integer multiple of some basic frequency $f_0$. In a typical musical note, multiple harmonics are present in varying proportions. For example, the signal played by a key (A minor) of a piano is plotted below:

The time series representation of a piano signal is given by

$$\text{y}(t) = \sum_{n=1}^{N} b_n \sin(2 \pi kf_0 t) e^{-\frac{t}{\tau}}$$

On performing Fourier analysis, the presence of fundamental frequency $f_o = 440$ Hz and their harmonics $k f_0$ can be seen. A piano note can be synthetically generated by combining all these harmonics (with appropriate weights) and applying an amplitude envelope.

Musical notes

A tune consists of a sequence of musical notes in succession. Each note consists of the fundamental frequency and its harmonics in a specified proportion (depending on the musical instrument). Each note can be of different duration within the tune.

Musical octaves

In musical terminology, an octave corresponds to doubling of the fundamental frequency $f_0$.

Try this sequency of $f_0$ to generate a tune corresponding to an octave of musical notes.