False Position

False Position (also called the linear interpolation method) is another well known bracketing method. It is very similar to bisection with the exception that it uses a different strategy to come up with its new root estimate. Rather than bisecting the interval, it locates the root by joining f(x₂) and f(x₁) with a straight line (Fig 1). The intersection of this line with the x axis represents an improved estimate of the root. Thus, the shape of the function influences the new root estimate. Using similar triangles, the intersection of the straight line with the x axis can be estimated as,
x3 = x1 - f(x1) * ((x2 - x1) / (f(x2) - f(x1)));        ...(eq. 1)

This is the False Position formula. The value of x<sub>3</sub> computed with (eq. 1), then replaces whichever of the two initial guesses, x<sub>2</sub> or x<sub>1</sub>, yields the funtion value with the same sign as f(x<sub>3</sub>). In this way, the values of x<sub>2</sub> and x<sub>1</sub> always bracket the true root. The process is repeated until the root is estimated adequately.
          

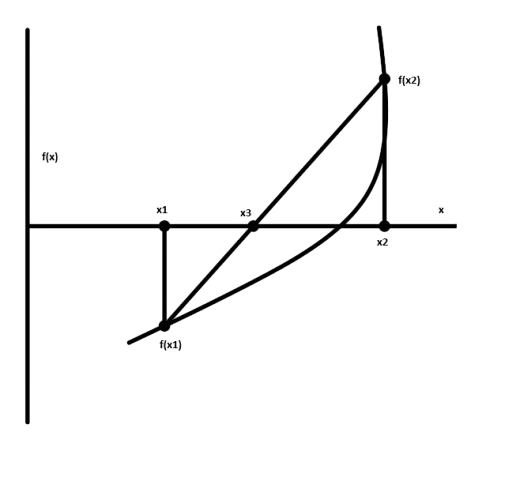
Fig 1