Theory

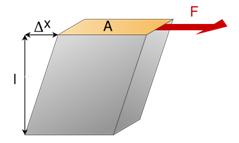
Shear modulus, or rigidity modulus n is defined as the ratio of stress F/A to strain $$\Delta x/l$$ when a shearing force F is applied to a rigid block of height l and area A. $$\Delta x$$ is the deformation of the block, and

This is similar to what happens when a torque $$\tau$$ is applied to a rigid rod of length l and radius r. Looking at the cross-section of the rod, consider a ring of width dr' at radius r' , which will have area $$2\pi r'dr'$$, with force applied tangentially. The weighted average force over the cross-sectional area A of the rod is then

$$\frac{1}{A}\int_{0}^{r}\frac{\tau}{r'}2\pi r'dr'=\frac{1}{\pi r^{2}}2\pi r\tau = \frac{2\tau}{r}........(2)$$

If the torque deforms the rod by twisting it through a small angle $$\theta$$, the deformation distance (corresponding to $$\Delta x$$) at the outside edge of the rod is approximately $$2\pi r$$. The definition of the rigidity modulus n becomes

$$n=\frac{F/A}{\Delta x/l}=\frac{\frac{2\tau}{r}/\pi r^{2}}{\theta r/l}=\frac{2\tau l}{\pi r^{4}\theta} .......(3)$$

In our apparatus the torque $$\tau$$ is supplied by hanging a weight of mass M from a string wound round a pulley of radius R, so $$\tau = MgR$$ and our definition of rigidity modulus n becomes

$$n=\frac{2MgR}{\pi r^{4}}\frac{l}{\theta}.......(4)$$

Now suppose we mount a small mirror on the rod at distance l from its fixed end, and look at a centimeter scale in the mirror through an adjacent telescope, both at distance D from the mirror. When the rod deforms and the mirror rotates through a small angle $$\theta$$, we look at a point on the scale a distance approximately $$S=2D\theta$$¸ from the original point, which was aligned with the telescope. We can measure D and S and substitute $$\theta =S/2D$$ in our definition of rigidity modulus n, to get

$$n=\frac{4MgR}{\pi r^{4}}\frac{lD}{S}.......(5)$$

Application

Engineers consider the value of shear modulus when selecting materials for shafts, which are rods that are subjected to twisting torques.