Red Black Tree
Structure of Red Black Tree
Each node contains the following fields:
- Key
- Left – pointer to the root of left subtree.
- Right – pointer to the root of right subtree.
- Parent – pointer to the parent node.
- Color- color of the node, either RED or BLACK
Properties of Red Black Tree
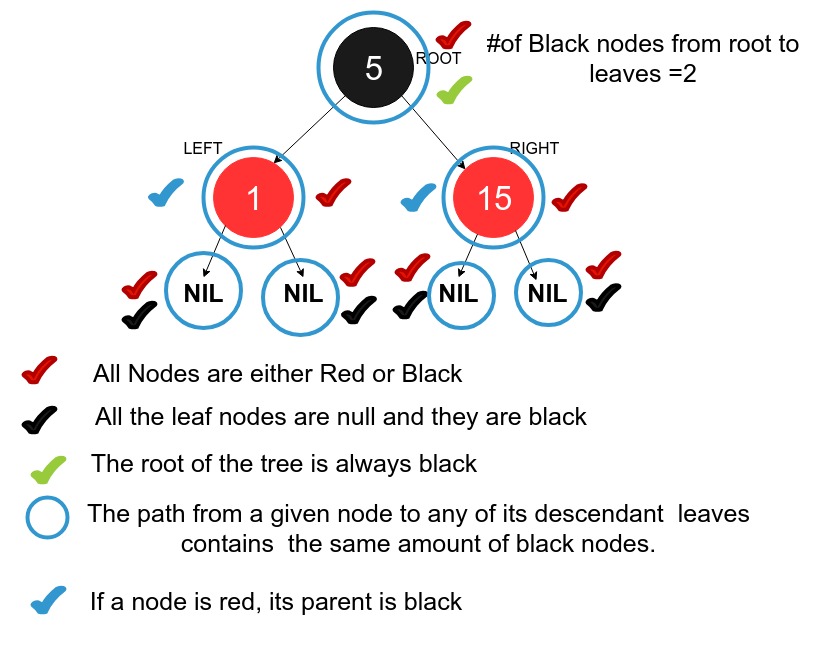
- Each node is either red or black.
- The root of the tree is always black.
- All leaves are null (Depicted as NIL in diagrams) and they are black.
- If a node is red, then its parent is black.
- Any path from a given node to any of its descendant leaves contains the same amount of black nodes. This is sometimes known as the black-depth.
Why do we impose such properties ?
- Binary Search Tree in worst can can have a complexity of O(n) in insert and delete. The Red-Black trees guarantee a O(log(n)) in insert, delete (even in worst case).
- They are balanced search trees and therefore balance themselves to always maintain a height of log(n),due to such restrictions.
Pictorial Representation of properties of a Red Black Tree