Q meter Experiment 
Introduction
The determination of the storage factor Q is one of the most widely used means in the laboratory for testing radio frequency coils, inductors and capacitors. The storage factor is equal to
$$ Q= \frac{\omega_0 L}{R} \quad where \quad \omega_0 $$
is the resonant frequency, L is the inductance and R is the effective resistance of the a coil. The effective resistance R, is never determined directly since its value depends upon the value of frequency.
Principle of Working:
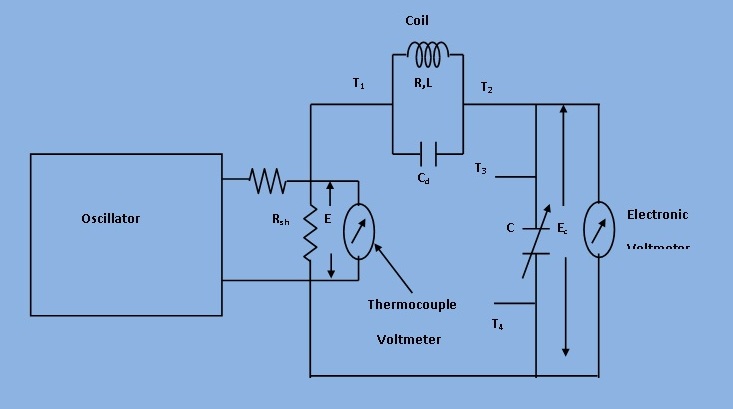
Fig 1: The practical circuit of unknown coil
Theory
The principle of working of this useful laboratory instrument is based upon the well-known characteristics of a resonant series R-L-C circuit.
At resonant frequency f0, we have XC = XL where capacitive reactance
$$ X_C = \frac{1}{2 \pi f_0 C} , \ inductive \ reactance \ X_L = 2 \pi f_0 L , \ resonant \ frequency \ f_0 = \frac{1}{2 \pi \sqrt LC} \ and \ current \ at \ resonance I_0 = \frac{E}{R} $$
$$ \ The \ voltage \ across \ the \ capacitor \quad E_C = I_0 * X_C=I_0 * X_L = I_0 * \omega_0L $$
and input voltage
$$ \quad E=I_0*R \quad then \quad \frac{E_C}{E}=\frac{\omega_0L}{R}=Q \quad and \quad E_C=QE $$
If the input voltage is kept constant the voltage across capacitor is Q times E and a voltmeter connected across the capacitor can be calibrated to read the value of Q directly.
Practical Circuit:
The practical circuit is shown in Figure 1. It consists of self contained variable frequency RF oscillator. This oscillator delivers current to a low value shunt resistance Rsh: value may be 0.02 Ohm. The small value of input voltage E is injected into circuit that would be measured by thermocouple voltmeter. An electronic voltmeter is connected across this capacitor. The coil under test is connected to terminals T1 and T2.
Measurement of Q:
The circuit for measurement of Q shown in Figure 1. The oscillator is set to the desired frequency and then the tuning capacitor is adjusted for maximum value E0. The input voltage E is kept constant then the voltage across capacitor is calibrated to read the value of Q directly. The measured value of Q is defined whole circuit not of the coil. There are errors caused due to shunt resistance and distributed capacitance of the circuit.
Correction of Shunt Resistance:
$$ Q_(meas) =\frac{\omega_0L}{R+R_(sh)}...............(1) $$
$$ True value, Q_(true)=\frac{\omega_0L}{R}=Q_(meas)(\frac{1+R_(sh)}{R}) $$
Correction of Distributed Capacitance:
$$ Q_(true)=Q_(meas)(1+\frac{C_d}{C})......(2) $$
Where, Cd=distributed capacitance and C=tuning capacitance.
Measurement of Self Capacitance:
The value of Inductance is given by
$$ L=\frac{1}{4 \pi^2f_0^2C}.................(3) $$
The values of f0 and C are known and therefore the value of inductance may be calculated.
Measurement of Effective Resistance:
The value of effective resistance may be computed from the relation
$$ R=\frac{\omega_0L}{Q_(true)}......(4) $$
Measurement of Self Capacitance:
The self capacitance is measured by making two measurements at different frequencies. The capacitor is set to a high value and the circuit is resonated by adjustment of the oscillator frequency. Resonance is indicated by the circuit Q meter. Let the values of tuning capacitor be C1 and that of frequency be f1 under these condition. Therefore,
$$ f_1=\frac{1}{2 \pi \sqrt(L(C_1+C_d))}...............(5) $$
The frequency is now increased to twice its initial value and the circuit is resonated again this time with the help of the tuning capacitor. Let the values of tuning capacitor be C2 and that of frequency be f2 under these condition. Therefore,
$$ f_2= \frac{1}{2 \pi \sqrt(L(C_2+C_d))}...............(6) $$
Now, f2=2*f1
The distributed capacitance,
$$ C_d=\frac{(C_1-4C_2)}{3}..............................(7) $$
