Theory

Pulse Amplitude Modulation (PAM) is a modulation technique where the amplitude of a series of regularly spaced pulses (the carrier signal) is varied in proportion to the instantaneous amplitude of the message signal. In simpler terms, the message information is encoded in the amplitude of these pulses. PAM is a foundational technique for digital communications and serves as a basis for other digital modulation methods.

Generation of a PAM Signal

The generation of a PAM signal involves two primary operations:

1. Sampling: The continuous-time message signal, m(t), is sampled at regular intervals, denoted by the sampling period, Ts. The sampling rate, fs = 1/Ts, must adhere to the Nyquist theorem to avoid aliasing, which is the distortion of the signal due to under-sampling. To prevent aliasing, the message signal is often first passed through a low-pass filter.
2. Amplitude Modulation of Pulses: The amplitude of each pulse in a pulse train is then modulated based on the corresponding sample value of the message signal.

The resulting PAM signal, \(s(t)\), can be expressed mathematically as:

where:

• \(m(nT_s)\) is the sample of the message signal at time \(t = nT_s\).
• \(h(t)\) is the shape of the pulse.
• The summation is over all integer values of \(n\).

Block Diagram

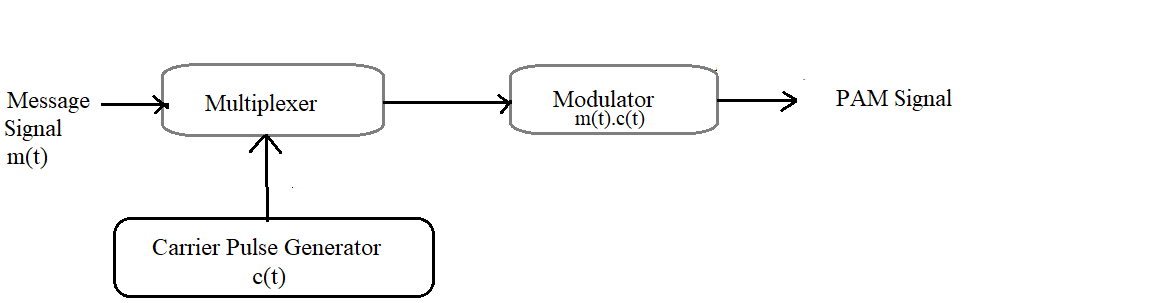
Fig: Pulse Amplitude Modulation Signal

Demodulation of a PAM Signal

Demodulation is the process of recovering the original message signal from the modulated PAM signal. For analog PAM, this is typically achieved by passing the PAM signal through a low-pass filter. The low-pass filter smooths out the high-frequency components of the pulses, effectively reconstructing the original analog message signal.

In digital PAM, demodulation involves detecting the discrete amplitude level of each pulse at specific time intervals. This is often done by sampling the received signal at the correct instants and comparing the sampled values to predefined thresholds to determine the transmitted symbol.

Digital PAM (M-ary PAM)

In digital communication, the number of possible pulse amplitudes is finite and is typically a power of two. This is known as M-ary PAM, where M represents the number of distinct amplitude levels. For example:

• 2-Level PAM (2-PAM or Binary PAM): Uses two amplitude levels, often representing binary 0 and 1.
• 4-Level PAM (4-PAM): Uses four distinct amplitude levels to represent two bits of information per pulse (2² = 4).
• 8-Level PAM (8-PAM): Uses eight distinct amplitude levels to represent three bits of information per pulse (2³ = 8).

Effect of Noise on PAM

Noise is an unavoidable aspect of communication channels. Since the information in PAM is encoded in the amplitude of the pulses, it is susceptible to noise that affects the signal's amplitude. This makes PAM's noise immunity lower compared to other modulation techniques like Pulse Width Modulation (PWM) or Pulse Position Modulation (PPM). The interference from other transmitted symbols, known as Intersymbol Interference (ISI), can also introduce errors in the received signal.

Applications of Pulse Amplitude Modulation

PAM is a fundamental technology with a wide range of applications, including:

• Ethernet Communications: Various Ethernet standards, such as 100BASE-T4 (PAM-3) and 1000BASE-T (PAM-5), utilize PAM for high-speed data transmission.
• Digital Subscriber Line (DSL): DSL modems use PAM to transmit digital data over telephone lines.
• Fiber Optic Communications: PAM is used to send digital data over optical fibers.
• Microcontrollers: PAM is used for generating control signals in many microcontrollers.
• LED Lighting: It is used as an electronic driver for LED lighting.
• Biomedical Signal Processing: PAM is employed for transmitting physiological signals like electrocardiograms (ECG).