Starting with 3-D space.

For a given point in a 3-D space, first, we should have measurements from the data given and have an orthographic projection, following the conventions properly.

Here basically, there are two measurements we must require for the projection of point:

1. The distance of a point from the vertical plane, the distance we observed from the top view.

2. The distance of a point from the horizontal plane, distance observed from the front view.

X Y

So, this is the orthographic 2-D plane on which the measurements are transferred. And now the next important part is a convention, which one has to follow while drawing.

Convention:-

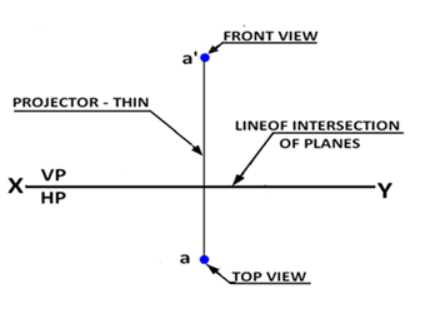
• Top views are represented by only small letters eg. p*.*

• Their front views are conventionally represented by small letters with dashes eg. p΄

• Profile or side views are represented by small letters with double dashes eg. p΄΄

• Projectors are shown as thin lines.

• The line of intersection of HP and VP is denoted as X-Y.

• The line of intersection of PP and VP is denoted as X1-Y1

• Measurements of projectors should also be drawn by side.

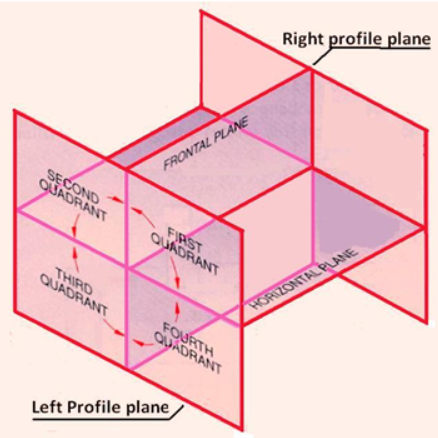
If we go for 3D space, it is divided into four quadrants. For every quadrant, there is a different orthographic projection.

• First quadrant: Projection on VP will be represented above XY line and HP will be below.

• Second quadrant: Projection on VP and HP both will be represented above XY line.

• Third quadrant: Projection on VP will be represented below XY line and HP will go above.

• Fourth quadrant: Projection on VP and HP both will go below XY line.

OBSERVER’S PERSPECTIVE

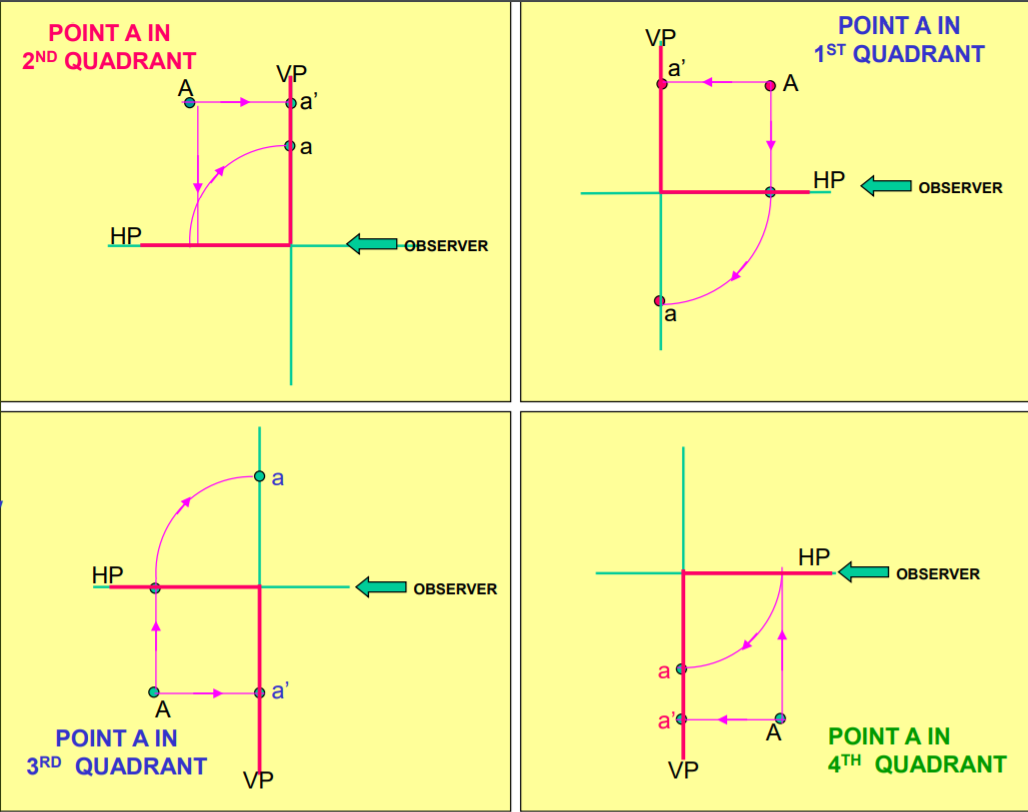
Envision a scenario in which Point A is positioned within distinct quadrants of a three-dimensional space. This conceptualization aids in understanding the spatial dynamics and distribution of points within a Cartesian coordinate system, providing a foundational basis for further exploration in spatial analysis and geometric interpretations. To make it easier for an observer to see both the Front View (FV) and Top View (TV) of Point A in a single plane, we need to rotate the TV 90 degrees clockwise.

• FV: It remains unchanged since it's a view on the Vertical Plane (VP).

• TV: Being a view on the Horizontal Plane (HP), it needs to be rotated. The part of the HP in front of the Vertical Plane (VP) now appears below the XY line, and the part behind the VP appears above.

By observing this process, you'll understand how the 3D perspective of Point A can be represented in a 2D plane for better visualisation