Polynomial Arithmetic

Multiplication of Polynomials using Linked list Theory

• In this approach we will multiply the 1st polynomial with each term of 2nd polynomial.
• Store the multiplied value in a new linked list.
• Then we will add the coefficients of elements having the same power in resultant polynomial.

Polynomial Multiplication using Linked list

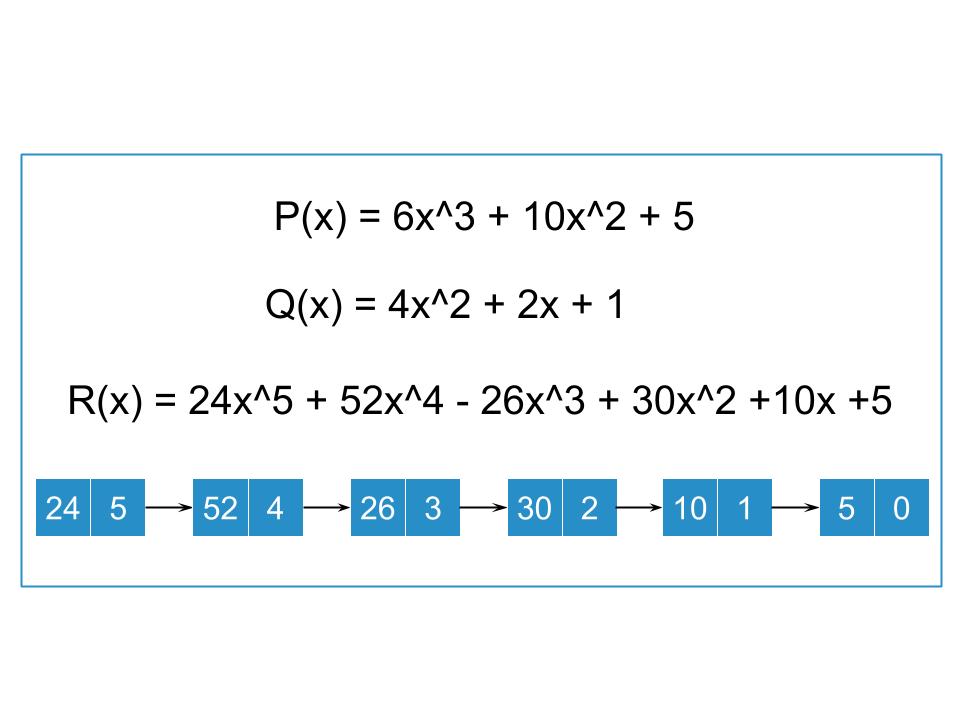
Here’s a simplified explanation:

1. Represent the two input polynomials as linked lists (poly1 and poly2).
2. Initialize a new linked list (result) for the resulting polynomial.
3. For each term in poly1:
   • Traverse poly2.
   • Multiply the terms and add the resulting term to result.
4. Traverse result to merge terms with the same exponent.
5. Return the result.

Following pseudocode will help in better understanding of the algorithm

Function multiplyPolynomials(poly1, poly2):
              result = NULL  // Initialize the result polynomial as an empty linked list
          
              // Traverse the first polynomial
              current1 = poly1
              While current1 is not NULL:
                  // Traverse the second polynomial
                  current2 = poly2
                  While current2 is not NULL:
                      // Multiply the terms
                      coeff = current1.coeff * current2.coeff
                      exp = current1.exp + current2.exp
          
                      // Add the resulting term to the result polynomial
                      result = addTerm(result, coeff, exp)
          
                      current2 = current2.next
                  End While
                  current1 = current1.next
              End While
          
              return result
          

Function addTerm(result, coeff, exp):
              // Case 1: If result is empty, create a new node
              If result == NULL:
                  result = createNode(coeff, exp)
                  return result
          
              // Case 2: Traverse result to find the right position or matching exponent
              current = result
              previous = NULL
              While current is not NULL:
                  If current.exp == exp:
                      // Combine like terms
                      current.coeff = current.coeff + coeff
                      return result
                  Else If current.exp < exp:
                      // Insert new term before the current term
                      newNode = createNode(coeff, exp)
                      If previous == NULL:
                          newNode.next = result
                          result = newNode
                      Else:
                          previous.next = newNode
                          newNode.next = current
                      return result
                  End If
                  previous = current
                  current = current.next
              End While
          
              // Case 3: Add the new term at the end
              newNode = createNode(coeff, exp)
              previous.next = newNode
              return result