Mass Moment Inertia of Pendulum
Procedure
In real Laboratory
For Simple Pendulum
- Suspend a point mass m from a fixed pivot point using a massless, inextensible string or rod of length L.
- Measure the length L from the pivot to the center of the mass accurately.
- Displace the pendulum by a small angle (less than 15°).
- Release the pendulum.
- Record the time for 10 complete oscillations to reduce timing errors.
- Calculate the period T by dividing the total time by the number of oscillations.
- Use the formula I = mL² to calculate the theoretical mass moment of inertia.
- verify the length L with the formula using the measured period T.
For Compound Pendulum
Attach a rigid body (e.g., a rod, disk, or rectangular plate) to a fixed horizontal pivot.
Measure the mass M of the rigid body.
Measure the dimensions of the rigid body.
Determine the distance h from the pivot to the center of mass.
Calculate the theoretical moment of inertia about the center of mass.
Displace the compound pendulum by a small angle.
Release the pendulum and record the time for 10 complete oscillations.
Calculate the period T by dividing the total time by the number of oscillations.
Using formula :
Calculate the experimental mass moment of inertia.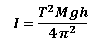
Calculate the moment of inertia using the parallel axis theorem I=Icm+Mh².
Compare the experimental moment of inertia with the theoretical value.
In Simulation
In a real experiment, the theoretical mass moment of inertia may be approximately estimated by measuring the approximate mass of different simplified geometrical components and adding the Mass Moment of Inertia about the central axis.
- Select the type of pendulum using the radio buttons.
- Adjust the initial setup parameters using the sliders to calculate the theoretical moment of inertia of the pendulum.
- Click the "Release" button to start the pendulum’s oscillations.
- The simulator will count the number of oscillations and the time period of each oscillation, and calculate the moment of inertia, displaying the results