Introduction

Minimax algorithm is a game search algorithm, which is used to determine optimal move for each player while playing a strategy game. It can be used in a 2 player game where the players take chances in alternative fashion. In Minimax algorithm one player is a maximizer and other minimizer. Maximizer tries to get the highest score possible while the minimizer tries to do the opposite and get the lowest score possible. For applying Minimax algorithm we convert the game into a tree and label the terminal nodes. The tree basically denotes the move the player can take in his chance from the current state he is in.

Tree Formation

We will take an example of Tic-Tac-Toe. Let the 2 players be cross (X) and nought (O). So here we can define cross as the maximizer and nought as the minimzer (can be defined otherwise as well). The aim is for cross to have the 3 X's in a straight line and prevent nought from having 3 O's in a straight line. It is exactly opposite for the nought. So basically, both players try to win by preventing other player to win the game. In these cases Minimax algorithm can be used. Let's see how we can define the Tic-Tac-Toe states to a tree. So, first we will create a tree of the Tic-Tac-Toe states until they converge by taking all possible moves from each state. Now we will label the terminal states with some numbers. If cross wins in the terminal state then we can have the state as 10 else if nought wins we can have it as -10 else 0. Now basically this implies that cross wants to maximize by getting a 10 whereas nought wants to minimize by getting -10. But, in this case when there can be 2 paths in a tree that can lead to a win for cross then any of the path can be chosen, although we want it to terminate as quickly as possible. So for this we use depth to mark terminal states. If cross wins then (10-depth) else if nought wins then (depth-10) else 0 (Note 10 is actually used because max depth is 9, when we start from no filled state). Using depth we will prefer the path where depth is less.

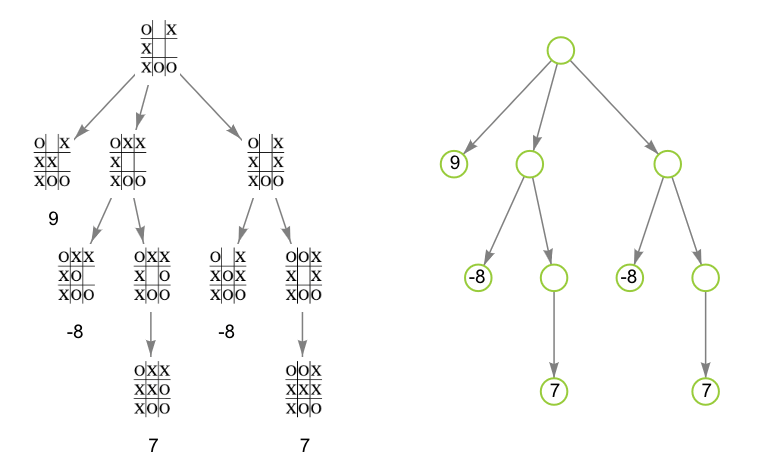
Algorithm

To be able to determine the optimal moves, Minimax algorithm needs to make a complete traversal of the tree using depth first search. We know that for a player to chose the next move he needs to know which move will lead to a maximum score if he is a maximizer and which move will lead to a minimum score if he is a minimizer. Therefore depth first search is required so that the Minimax search algorithm can proceed all the way down to the terminal nodes of the tree and then select the optimal move from the child nodes while backtracking the tree. We know that maximizer will pick max of the child nodes whereas minimizer will pick min of the child nodes. So based on this we calculate and assign the value for the states and build to the top while backtracking.

Advantages

Can be used to solve a large number of games such as Go, Tic-Tac-Toe, Chess etc.

Disadvantages

Sometimes there are a large number of states in a game and we know the number of states are in exponential order of depth, so in those cases we can use alpha beta pruning as an optimization strategy to reduce the number of states that are considered in the minimax algorithm.