Introduction

Iterative Deepening Depth-First Search (IDDFS) is an uninformed search algorithm that is used to explore or search through a graph. The key feature of IDDFS is its iterative approach, where the depth limit is progressively increased during each iteration. This method combines the memory efficiency of Depth-First Search (DFS) with the completeness and optimality properties of Breadth-First Search (BFS). IDDFS is particularly effective for large graphs where the depth is unknown or potentially infinite.

Algorithm

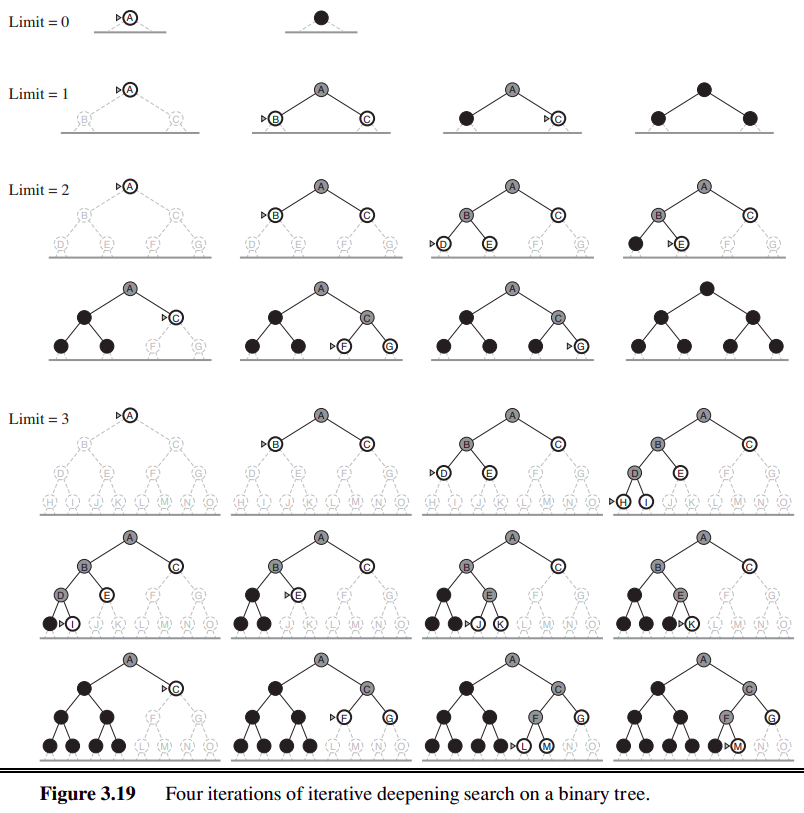
IDDFS is a strategy where a depth-limited search is performed iteratively with increasing depth limits until the goal node is found. The algorithm uses Depth-First Search (DFS) at each iteration but restricts the search to a specific depth.

STEP 1: Set the initial depth limit to 0.

STEP 2: Perform a Depth-Limited Depth-First Search (DLDFS) from the starting node, restricting the search to the current depth limit. In DLDFS, the search is confined to a maximum depth, and nodes beyond that depth are not considered.

STEP 3: If the goal node is encountered during DLDFS, return the path from the start node to the goal node.

STEP 4: If the goal node is not found within the current depth limit, increase the depth limit by 1 and repeat steps 2 and 3.

STEP 5: If the goal node is not found and the depth limit exceeds a predefined maximum depth or the depth of the tree, terminate the search process.

Example

Reference: Section 3.4.5 of Reference 1

Optimality and Completeness

Optimality: Since IDDFS explores the graph level by level (depth by depth), it will always find the shallowest solution first. In other words, it will first find the goal that is closest to the root in terms of depth, as it explores all nodes at depth 0, then depth 1, and so on. IDDFS guarantees that once it finds a solution, that solution is the shallowest possible solution because it explores all nodes at a lower depth before increasing the search depth.

Completeness: IDDFS is complete for finite graphs. It exhaustively searches the entire search space, incrementally increasing the depth limit with each iteration until the goal node is found or until the maximum depth limit is reached. As long as the branching factor is finite and the depth limit is sufficient, IDDFS will find a solution if one exists.

Space and Time Complexity

The space complexity of IDDFS is the same as DFS - $O(bm)$, where b is the branching factor and m is maximum depth limit. IDDFS may seem like it will have a high time complexity as states are generated multiple times. However, this is not the case. This is because the nodes at the bottom level (depth d) are generated once, those on the next to bottom level are generated twice, and so on, up to the children of the root which are generated d times. So the total number of nodes generated in the worst case is:

$N(IDDFS) = (d)b + (d-1)b^2 + ... + (1)b^d$,

which gives a time complexity of $O(b^d)$ - asymptotically the same as Breadth-First Search. There is some extra cost for generating the upper levels multiple times, but it is not large.

Reference: Section 3.4.5 of Reference 1

Advantages

Memory Efficiency: IDDFS requires less memory compared to breadth-first search, as it explores nodes in a depth-first manner and discards unnecessary nodes as it increases the depth limit.

Large Search Spaces: In general, IDDFS is the preferred uninformed search method when the search space is large and the depth of the solution is not known. It performs better than DFS which might unnecessarily explore a large subtree before reaching the goal node.

Disadvantages

Time Complexity: IDDFS may have high time complexity, especially for large graphs or when the optimal solution is deep in the search tree. It may repeat work at each depth level, leading to inefficiency.

Completeness: IDDFS is not complete for infinited graphs. It may not be suitable for graphs with unknown depths, as it required specifying a maximum depth limit.

Optimality: IDDFS does not necessarily find the shortest path or the most optimal solution. It is only optimal if the step costs are a non decreasing function of the depth of the node.