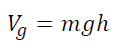CONSERVATION OF MECHANICAL ENERGY WITH SLIDING MOTION
THEORY
This experiment is an introduction to investigate the concepts of friction, work, kinetic and potential energy conservative forces and the conservation of energy
Frictional Force in Inclined Plane
When this object is resting on a level surface, its weight W of the object that acts through the centre of gravity will be directed towards the centre of the Earth and perpendicularly to the surface. The surface will exert an equal amount of force termed as the normal force perpendicular to the surface. The body is in equilibrium since the normal force prevents the object from falling through the surface. Now when
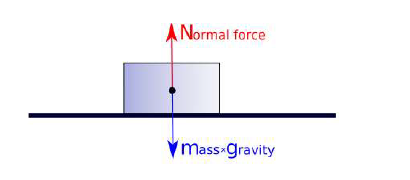
Now when the surface is inclined, the same weight W still acts on it, but the normal force will be a fraction of the weight (as the weight can be resolved into individual components perpendicular to the plane and parallel to the plane). This is illustrated in the figure below.
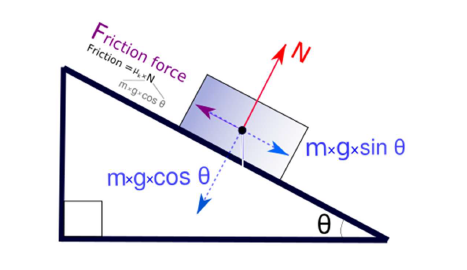
In addition to the above forces, an additional force comes into picture due to the relative contact between the object surface and the plane. This force always acts tangent to the surface at the points of contact and tries to oppose the motion between the surfaces. This force is called force of friction. If the body is idealised to be a particle in particle dynamics, the frictional force can also be assumed to be acting along the centre of mass Depending upon the numerical value of forces acting along the plane, the body may either be at rest or in motion. The numerical value of friction during equilibrium is different than that during motion. However in both cases, experiments have proved that F is directly proportional to the normal force N The frictional force on an object when not in motion is termed as the static frictional force FS and that during motion is called kinetic frictional force.
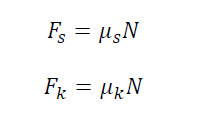
where the constant of proportionality μs and μk are called the coefficient of static friction and the coefficient of dynamic friction respectively. The friction coefficients are functions of the contact materials. The force necessary to induce motion (i.e. to overcome the static friction), is bigger than the one necessary to continue the motion (i.e. to overcome kinetic friction). So the coefficient of kinetic friction (μk) is lower than the one of static friction (μs). In short, an object kept on a tilted surface may either be at rest or slide down the plane depending upon the following factors
- Weight of the Object
- Angle of the inclined plane
- Coefficient of friction between the surfaces in contact
Work of Force
When a force is capable of producing a displacement on an object, it is said that work is done on the object. In other words, work is the energy transferred to or from an object via the application of force along a displacement. Work is a scalar quantity and is given by the dot product of the force and displacement vectors for
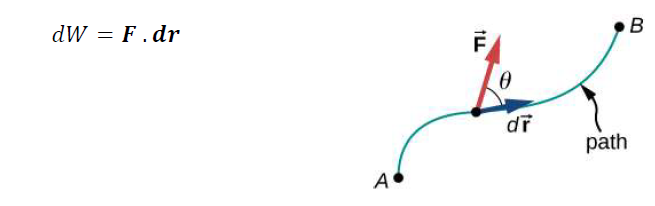
where dr is the infinitesimal vector displacement of the point of application of F. The total work done as a particle moves from point A to B is given as
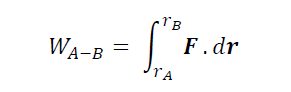
The work done may be as a result of conservative or non-conservative forces. A conservative force is a force that does zero work on a closed path. That is, the work done by conservative force in going from point A to point B is independent of the path from A to B. Examples of conservative forces include gravity and the spring force. In case of free sliding motion, the resultant force in the direction of displacement is constant throughout the motion. The magnitude of this tangential force ΣFT is given as
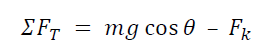
Therefore, the work done by sliding bodies can be given as
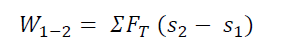
Kinetic Energy
Kinetic energy T is the energy possessed by body by virtue of its motion. The energy of motion can be due to translational and rotational motion of a body. In sliding bodies, the object is in translational motion and the translational kinetic energy is given by the equation.
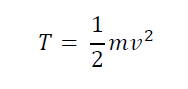
Where m is the mass of the object and v is its velocity So the work done on an object to change its position from point 1 to 2 results in a change in the kinetic energy of that object.
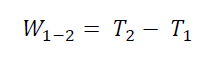
Potential Energy
Work done on an object may be as a result of externally applied forces, gravity forces, spring forces, electrostatic forces, etc. Work done by conservative forces such as gravity, elastic forces in spring and electrostatic forces depends only on the initial and final positions of the object along the path. For conservative forces, it is possible to specify a numerical value as a potential function of force depending upon its position of object in space. This energy possessed by an object by virtue of this position is called Potential Energy. In this experiment of sliding bodies, we deal with gravitational forces and hence the potential due to gravity. The gravitational potential energy Vg of the object is defined as the work done against the gravitational field to elevate the object by a height with respect to an arbitrary datum (where Vg is taken as zero). So, if an object is at a height y above the datum, the gravitational potential energy Vg can be given as