Procedure

Step 1: Understand and Analyze the Theorem

Observe and carefully read the Pumping Lemma theorem to grasp its conditions and implications for context-free languages.

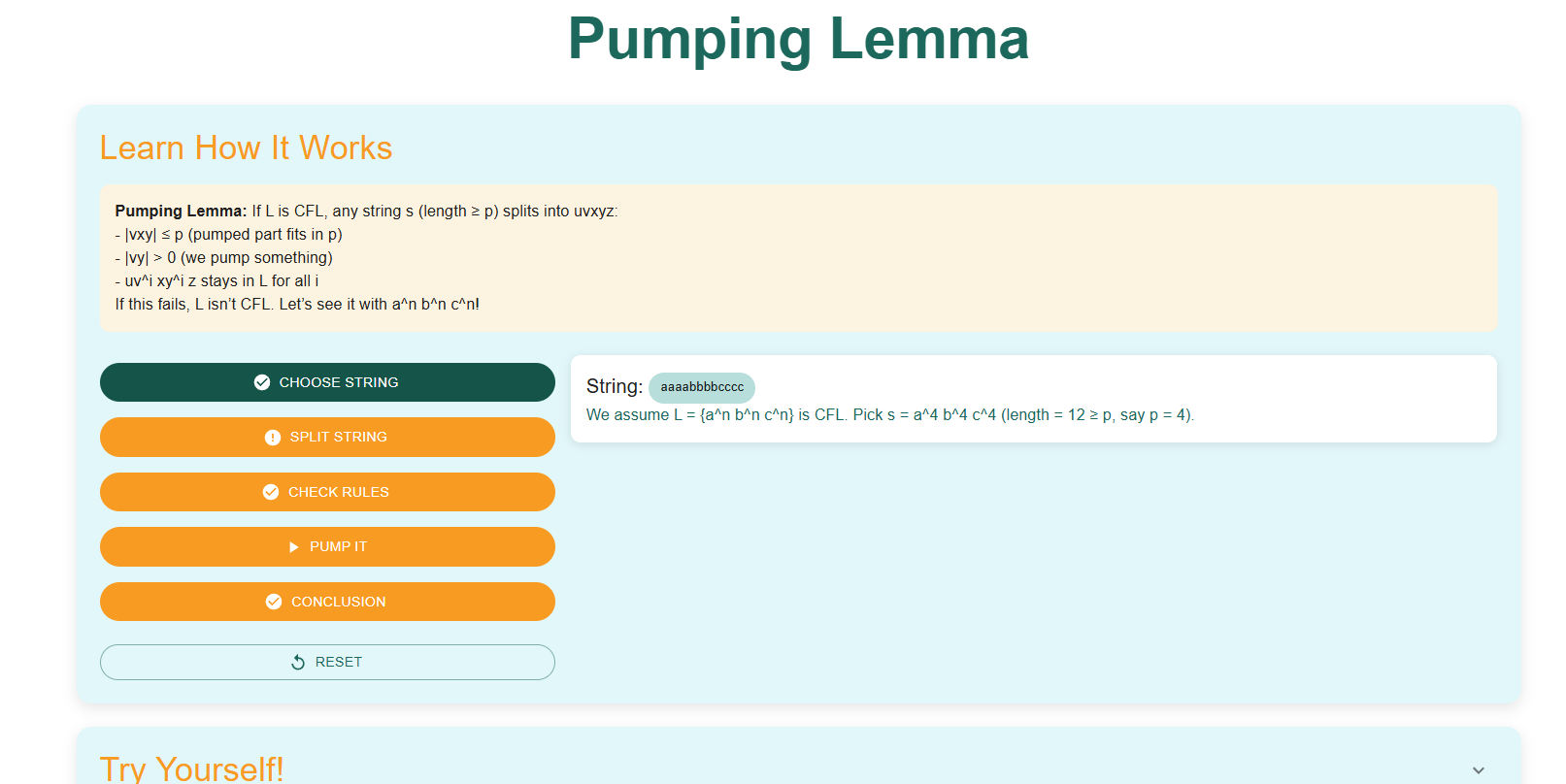
Step 2: Select a String

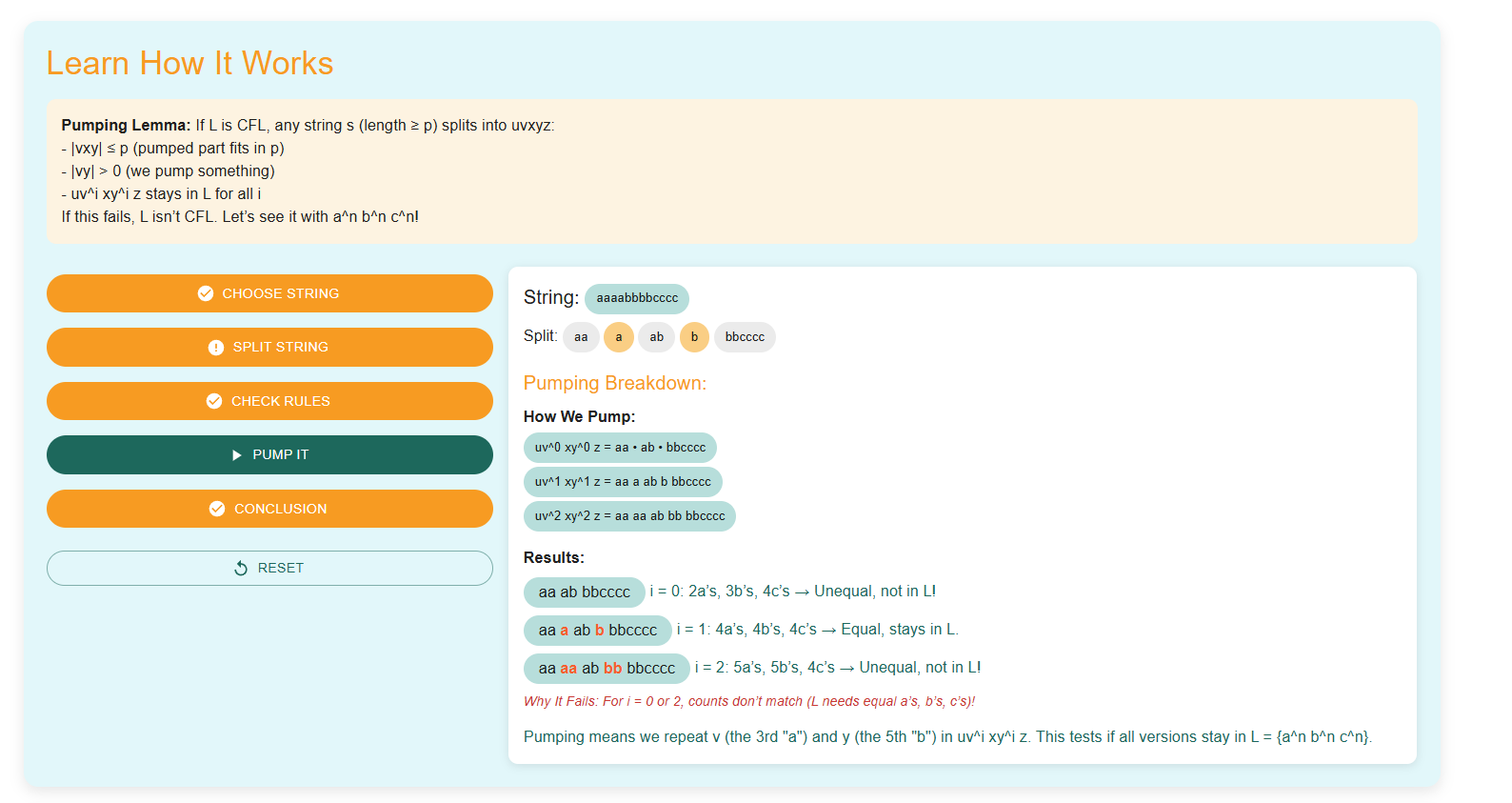
Click on the “Choose the String” button to start the process. Observe the string being created.

The Length (L) and Pumping Constant (p)

The length of the selected string is represented as L. In the Pumping Lemma, there is a special value called the pumping constant (p), which is a number given by the theorem. If a language is context-free, any string with a length L ≥ p must be able to be split and "pumped" while still remaining in the language.

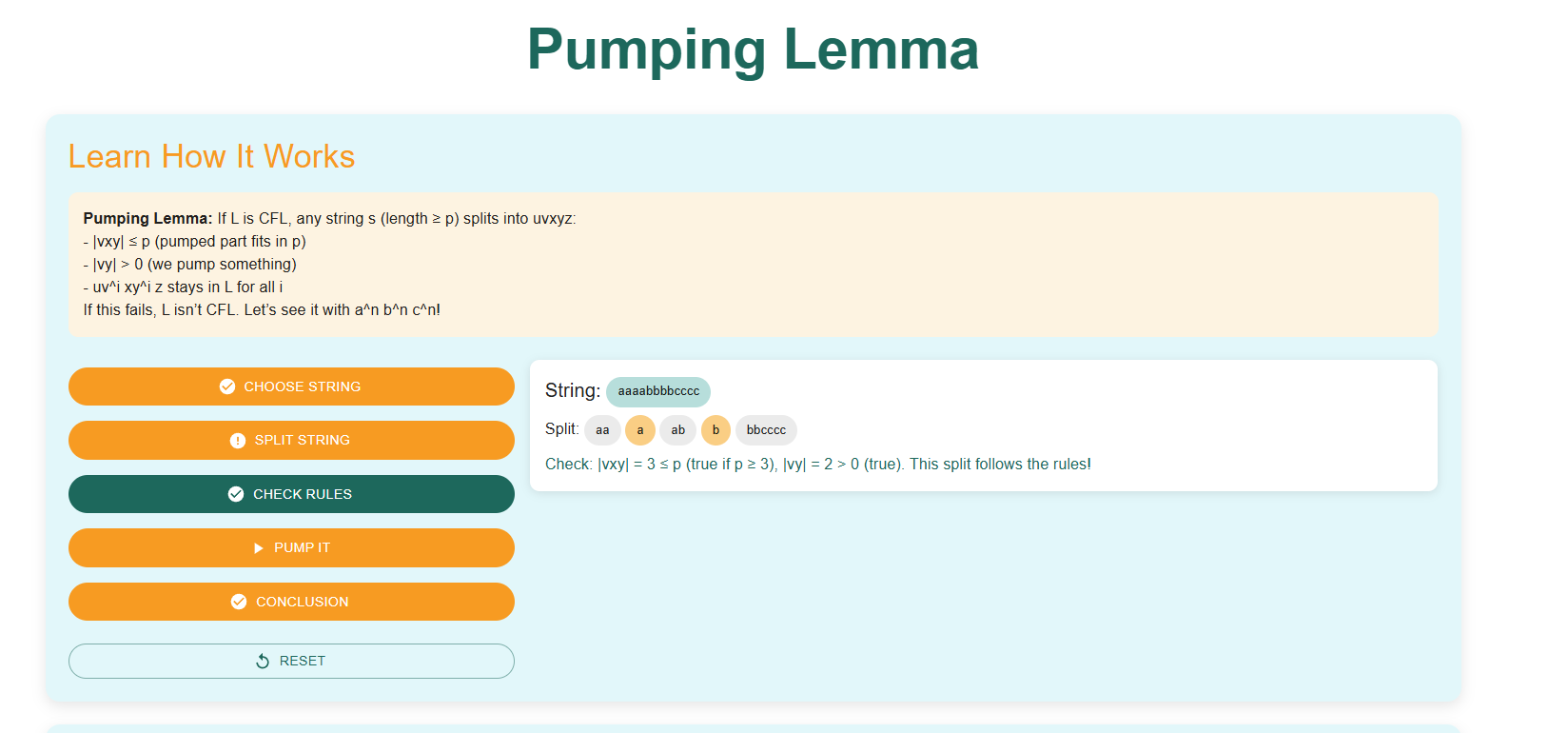
Step 3: Split the String

Divide the selected string into five parts: u, v, x, y, z, following the conditions of the Pumping Lemma. The decomposition should satisfy the given constraints, ensuring that v and y can be pumped while maintaining the language's properties.

Step 4: Verify the Pumping Lemma Conditions

Check if the decomposition (u, v, x, y, z) satisfies the Pumping Lemma rules:

• The length of the string must be at least p (pumping length).
• The string is divided into five parts: u, v, x, y, z.
• v and y must not be empty (|vy| > 0).
• vxy must be within the first p characters.
• The string must remain in the language for all values of i (pumping).

Step 5: Pump the String

Enter a value for i to pump the string. The substrings v and y will be repeated i times while keeping u, x, and z unchanged.

Observe how the modified string changes with different values of i and check if it still belongs to the given language.

Step 6: Click Conclusion for Final Results

Click on the “Conclusion” button to determine whether the given language is context-free.

Based on the results of the pumping process, check if the string still belongs to the language. If it fails the conditions, the language is not context-free.

Explore and Experiment

Use the Try Yourself section to test different strings and analyze their behavior using the Pumping Lemma.

Follow the steps, modify the pumping factor i, and observe how the string changes. Determine whether the language satisfies the context-free conditions.