Hamming Codes
In Experiment-2, we provided a brief introduction to linear block codes, their generator and parity-check matrices. In this experiment, we shall focus on a specific class of linear block codes known as Hamming codes. We will describe these codes, calculate the parameters for these codes, give a procedure for encoding and also a procedure for correcting single errors in a Hamming code.
The theory associated with Experiment-3 is divided into two parts:
- Encoding
- Error Correction
1. Encoding
We will now describe the encoding of Hamming code through a diagram of 3 circles as shown in Figure
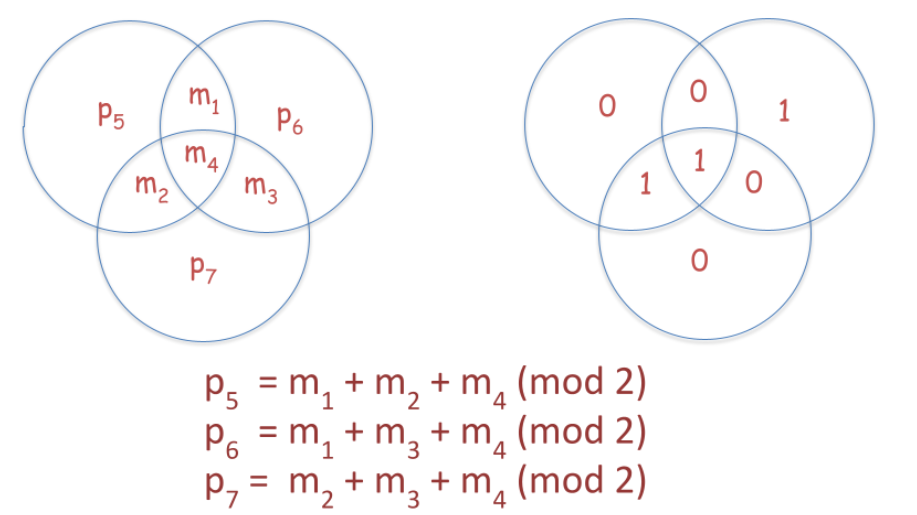
Figure 1: Diagram illustrating the encoding procedure for the (7,4) Hamming code.
Hamming code is a code over binary field of length 7, dimension 4 and minimum distance 3. The encoding procedure of the Hamming code is given by the following equations:
Please note that in the above equations, the addition is modulo-2 addition over the binary field. Based on the above equations, the generator matrix of the Hamming code is given by
The parity-check matrix of the Hamming code can be obtained by rewriting the equations as follows:
The parity-check matrix itself is given by
The minimum distance of a Hamming code is 3. This can be seen in one of the following two ways:
- Enumerate all possible codewords of the Hamming code and find the minimum Hamming weight of any codeword.
- In a second method, the minimum distance of a linear code can be obtained by determining the smallest number such that any columns of the parity check matrix are linearly independent. The minimum distance of a code in this case is . It can be seen from the parity check matrix of the Hamming code that the smallest number such that any columns of the parity check matrix are linearly independent is and hence the minimum distance of the Hamming code is .
2. Error Correction
Let the received binary vector be denoted by . We will give a decoding rule by which we can correct one error. Calculate the following quantities
If is , then it means that the parity equation is said to match and if is , then the parity equation is said to not match. Similar is the case with and .
Case 1: One parity equation does not match:
If is , then is received erroneously. If is , then is received erroneously. If is , then is received erroneously.Case 2: Two parity equations do not match:
If , then is received erroneously. If , then is received erroneously. If , then is received erroneously.Case 3: Three parity equations do not match:
If , then is received erroneously.
