Half Wave Rectification 
Theory
Rectification
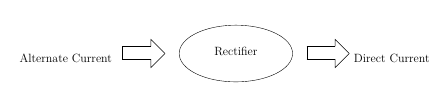
Figure 1
Half Wave Rectification
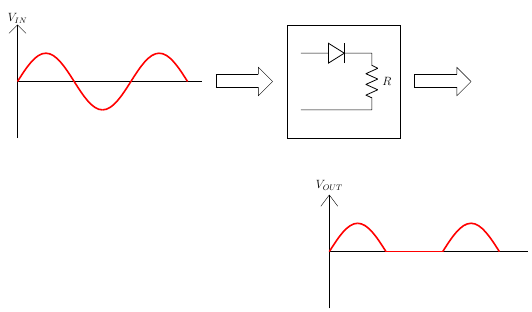
Figure 2
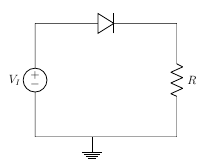
Figure 3
The simplest kind of rectifier circuit is the half-wave rectifier.The half-wave rectifier is a circuit that allows only part of an input signal to pass. The circuit is simply the combination of a single diode in series with a resistor, where the resistor is acting as a load.
Half Wave Rectifiers – Waveforms
Figure 4
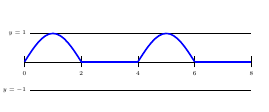
Figure 5
The output DC voltage of a half wave rectifier can be calculated with the following two ideal equations.
$$V_{peak}=V_{rms} \times √2$$ $$V_{dc}=\frac{V_{peak}}{Π}$$
Half Wave Rectification:For Positive Half Cycle
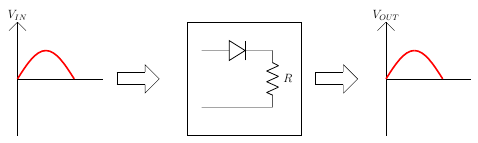
Figure 6
Diode is forward biased, acts as a short circuit, passes the waveform through.
For positive half cycle: $$V_I - V_b - I \times r_d - I \times R=0$$
where,
VI is the input voltage,
Vb is barrier potential,
rd is diode resistance,
I is total current,
R is resistance
$$I=\frac{V_I - V_b}{r_d + R}$$
$$V_O = I \times R$$
$$V_O =\frac{V_I - V_b}{r_d + R} \times R$$
For rd<< R,
$$V_O = V_I- V_b$$
Vb is 0.3 for Germanium ,
Vb is 0.7 for Silicon
For VI < Vb,
The diode will remain OFF.The Output voltage will be, VO =0 For $$V_I > V_b $$,
The diode will be ON.The Output voltage will be, $$V_O = V_I- V_b$$
Half Wave Rectification:For Negative Half Cycle
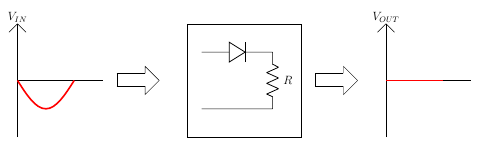
Figure 7
Diode is reverse biased, acts as a open circuit, does not pass the waveform through.
For negative half cycle:
$$V_O=0 \quad Since, \quad I =0$$
Half wave Rectification:For an Ideal Diode
For Ideal Diode, Vb = 0
For positive half cycle, VO = VI
For negative half cycle, VO = 0
Average output voltage
$$V_O=V_m \times \sin wt \quad for \quad 0 \leq wt \leq \pi$$ $$V_O=0 \quad for \quad \pi \leq wt \leq 2 \pi$$ $$V_{av}=\frac{V_m}{\pi} =0.318V_m$$
RMS load voltage
$$V_{rms}=I_{rms} \times R = \frac {V_m}{2}$$
Average load current
$$I_{av}=\frac{V_{av}}{R} =\frac{\frac{V_m}{\pi}}{R}$$ $$I_{av}=\frac{V_{m}}{\pi \times R}=\frac{I_m}{\pi}$$ RMS load current
$$I_{rms}=\frac {I_m}{2}$$
Form factor: It is defined as the ratio of rms load voltage and average load voltage.
$$F.F= \frac{V_{rms}}{V_{av}}$$ $$F.F= \frac{\frac{V_{m}}{2}}{\frac{V_{av}}{2}}=\frac{\pi}{2}=1.57$$ $$F.F \geq 1$$ $$rms \geq av$$
Ripple Factor
$$\gamma=\sqrt({F.F}^2-1) \times 100\%$$ $$\gamma=\sqrt({1.57}^2-1) \times 100\%=1.21\%$$
Efficiency:It is defined as ratio of dc power available at the load to the input ac power.
$$n \%=\frac{P_{load}}{P_{in}} \times 100 \%$$ $$n \%=\frac{I_{dc}^2 \times R}{I_{rms}^2 \times R}\times 100 \%$$ $$n \%=\frac{\frac {I_{m}^2}{\pi^2}}{\frac{I_{m}^2}{4}}\times 100 \%=\frac{4}{\pi^2}\times 100 \% =40.56 \%$$
Peak Inverse Volatge
For rectifier applications, peak inverse voltage (PIV) or peak reverse voltage (PRV) is the maximum value of reverse voltage which occurs at the peak of the input cycle when the diode is reverse-biased.The portion of the sinusoidal waveform which repeats or duplicates itself is known as the cycle. The part of the cycle above the horizontal axis is called the positive half-cycle, the part of the cycle below the horizontal axis is called the negative half cycle. With reference to the amplitude of the cycle, the peak inverse voltage is specified as the maximum negative value of the sine-wave within a cycle's negative half cycle.
$$ PIV=V$$ $$ -V_m +V=0 \Rightarrow V=V_m$$ $$PIV \geq V_m$$
