Group Theory
Introduction:
The symmetry relationships in the molecular structure provide the basis for a mathematical theory, called group theory. The mathematics of group theory is predominantly algebra. Since all molecules are certain geometrical entities, the group theory dealing with such molecules is also called the ‘algebra of geometry’.
Symmetry Element:
A symmetry element is a geometrical entity such as a point, a line or a plane about which an inversion, a rotation or a reflection is carried out in order to obtain an equivalent orientation.
Symmetry Operation:
A symmetry operation is a movement such as an inversion about a point, a rotation about a line or a reflection about a plane in order to get an equivalent orientation.
The various symmetry elements and symmetry operations are listed in the table below.
| Symmetry element | Symmetry operation | Schoenflies symbol | Hermann-Mauguin symbol |
|---|---|---|---|
| Centre of Symmetry or Inversion centre | Inversion | I | Ä® |
| Plane of symmetry | Reflection θ | σ | m |
| Axis of symmetry | Rotation through | Cn | n |
| Improper axis | Rotation followed by reflection in a plane perpendicular to axis | Sn | ñ |
| Identity element | Identity Operation | E |
Centre of Symmetry:
A point in the molecule from which lines drawn to opposite directions will meet similar points at exactly the same distance. Some of the molecules, which have a centre of symmetry, are:
- N2F2
- PtCl4
- C2H6
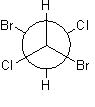
1,2-di chloro-1,2-di bromoethane(all trans and staggered)
Plane of Symmetry:
A plane which divides the molecule into two equal halves such that one half is the exact mirror image of the other half. The molecules, which have plane of symmetry, are:
- H2O
- N2F2
- C2H4
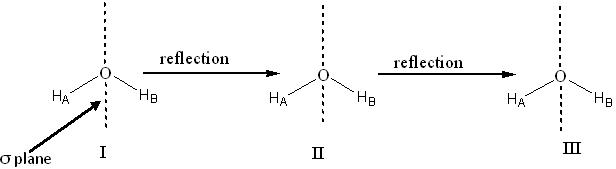
The broken line in the σ-plane: If we look from the left side (A) into the mirror plane, HA appears to have gone on the other side and its image appears exactly at HB. Similarly, viewing the structure of the H2O molecule from the right side (B), the reflection of HB appears at HA. Configuration II is the result of this reflection operation and is equivalent to I. Another round of this operation on the molecule (configuration II) yields configuration III, which is identical to configuration I.
Proper Axis of Symmetry:
An axis passing through the molecule about which, when the molecule is rotated 360°/n, an equivalent orientation is produced. This is an axis of n-fold symmetry or an axis of order, as shown below.
- H2O
- N2H3
- BF3
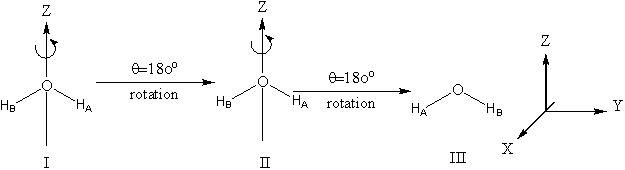
Initially, the H2O molecule is in configuration I, lying flat on the plane of the paper. After rotating it through an angle θ = 180° about an axis passing through the O atom (Z-axis) and along the HOH angle, configuration II is obtained. Configuration II is equivalent to configuration I, but not identical. A second, similar rotation about the Z-axis on configuration II results in configuration III. Configuration III is identical to the initial configuration I.
Principal Axis:
If there is more than one axis of symmetry, in many cases one of the axes is identified as the principal axis. This axis is selected in the following order:
- The only axis
- The highest order axis
- The axis passing through the maximum number of atoms
- The axis perpendicular to the plane of the molecule
The principal axis is taken as the vertical axis in the z-direction. The subsidiary axis is perpendicular to the principal axis and hence lies in the horizontal direction.
| Molecule | Principal Axis | Subsidiary Axis |
|---|---|---|
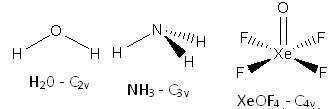
| Water | C2 | Nil |
| Ammonia | C3 | Nil |
| BF3 | C3 | 3C2 |
| XeF4 | C4 | 4C2 |
| Cyclopentadienyl anion | C5 | 5C2 |
| Benzene | C6 | 6C2 |
| H2O2 | C2 | Nil |
| XeOF4 | C4 | Nil |
(A Cn axis can combine with only n C2 axes perpendicular to it or with no subsidiary axis.)
The plane of symmetry is also classified based on the principal axis. Planes that include or involve the principal axis are called vertical planes (σv), and planes perpendicular to the principal axis are called horizontal planes (σh).
| Molecule | Principal Axis | Vertical Planes | Horizontal Planes |
|---|---|---|---|
| Water | C2 | Nil | Nil |
| Ammonia | C3 | Nil | One |
| BF3 | C3 | 2 | Nil |
| XeF4 | C4 | 3 | Nil |
| Cyclopentadienyl anion | C5 | 3 | One |
| Benzene | C6 | 4 | One |
| H2O2 | C2 | 6 | One |
| XeOF4 | C4 | 4 | Nil |
Improper Axis of Symmetry:
An axis passing through the object about which, when the object is rotated through 360°/n followed by reflection in a plane perpendicular to the axis, produces an equivalent orientation.
For example: Ethane molecule (staggered form).
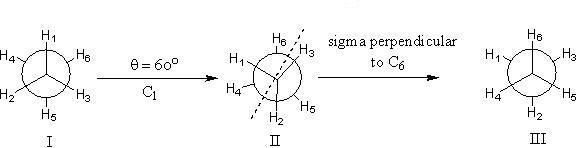
Configuration I and II are not equivalent, i.e., θ = 60°, and therefore the C6 rotational operation is not a valid symmetry operation by itself. Similarly, configurations II and III are not equivalent, indicating that the σ operation perpendicular to the so-called C6 rotational axis is also not a genuine symmetry operation. However, configurations I and III are equivalent, so that a C6 operation followed by a σ operation perpendicular to C6 constitutes a valid combined operation. This product operation results in an element called the S6 axis.
Identity Element:
This element is obtained by an operation called the identity operation. After this operation, the molecule remains unchanged. This situation can be visualized in two ways:
- We do not perform any operation on the molecule, or
- We rotate the molecule by 360°.
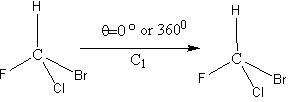
Every molecule has this element of symmetry, and it co-exists with the identity of the molecule; hence the name identity element.
Point Group:
The symmetry elements can combine only in a limited number of ways, and these combinations are called point groups.
Nomenclature of the Point Group:
- There are certain conventions developed by two schools of thought for naming these point groups.
- The Schoenflies nomenclature is more popularly used for molecular point groups than that of Hermann-Mauguin.
- Crystal and space groups are named using Hermann-Mauguin symbolism.
- For example, H2O and pyridine are assigned the point group symbol C2v, which means the molecules contain a C2 axis and 2 σv planes.
Identification of Molecular Point Groups:
The whole set of molecules can be divided into three broad categories:
- Molecules of Low Symmetry (MLS)
- Molecules of High Symmetry (MHS)
- Molecules of Special Symmetry (MSS)
Molecules of Low Symmetry (MLS):
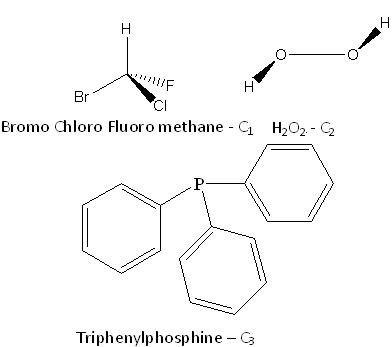
The starting point could be molecules containing no symmetry elements other than E. Such molecules are unsymmetrically substituted and belong to the C1 point group.
For example: TeCl2Br2 in its gaseous phase, and tetrahedral carbon and silicon compounds with the formula AHFClBr (A = C, Si), belong to the C1 point group.
Molecules of High Symmetry (MHS):
This category includes all molecules containing a Cn axis, either alone or with additional symmetry elements. The three main types of point groups are: Cn, Dn, and Sn.
Cn Type Point Group:
Molecules that contain only one Cn (proper) axis fall under the Cn point group. The presence of a Cn axis implies the presence of (n–1) distinct symmetry elements. Whether n is even or odd, a Cn operation generates a set of n symmetry elements including the identity E.
Thus, the order of the Cn group is n (h = n), and such molecules are designated as belonging to Cn point groups.
Cnv Point Groups:
This group contains a Cn axis and n σv planes of symmetry.
- When n is odd, all the planes are of the σv type.
- When n is even, there are n⁄2 planes of σv type and n⁄2 planes of σv′ type.
Cnh Point Groups:
This set of point groups is formed by adding a horizontal plane (σh) to a proper rotational axis, Cn.
The group has a total of 2n elements — n elements from the Cn operations, and the other n elements generated by combining Cn with σh, resulting in corresponding Sn axes.
When n is even, molecules belonging to the Cnh point group necessarily contain a centre of inversion (i).
Dn Point Groups:
These are purely rotational groups, meaning they contain only rotational axes of symmetry.
When a molecule contains only one Cn axis, it is classified under the Cn point group. However, if in addition to a primary Cn axis, there exists a set of n C2 axes perpendicular to the Cn axis, the molecule belongs to the Dn point group.
The order of this rotational group is 2n, since the Cn operations generate (n – 1) + E elements, and the n C2 axes contribute n additional operations.
For example, the gauche (skew) form of ethane belongs to the D3 point group.
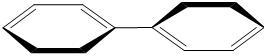
Biphenyl (skew) - D2
Dnh Point Groups:
This point group is formed by adding a horizontal mirror plane (σh) to the symmetry elements of a Dn group.
The order of the Dnh group is 4n.
- When n is even, the elements generated by the addition of σh are distinct and different from those already present in the Dn group.
- When n is odd, a set of n elements based on Sn axes is obtained.
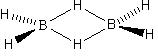
An example of a molecule in this point group is B2H6, which belongs to the D2h point group.
Dnd Point Groups:
This point group is obtained by adding a set of dihedral planes (nσd) to the elements of a Dn group.
To qualify for this point group, a molecule must possess:
- A Cn proper rotational axis
- n C2 axes perpendicular to the Cn axis
- n σd planes (dihedral mirror planes)
This results in a total of 3n symmetry elements at minimum.
An example is cyclohexane in chair conformation, which belongs to the D3d point group.

Sn Point Groups:
The Sn axis (improper rotation axis) is the sole group generator for the Sn point group, where n is even.
For n odd, the presence of an Sn axis implies the existence of 2n elements, which include a mirror plane (σ) that appears independently.
The presence of additional symmetry elements alongside the Sn axis leads to other point groups:
- If a plane perpendicular to the Cn or Sn axis is present, the molecule may belong to point groups like Cnh, Dnh, or Dnd.
- If n is even and there is no horizontal mirror plane (σh), but other elements exist along with Sn, the molecule most likely belongs to the Dnd point group.
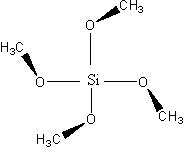
An example of a molecule belonging to this group is SiO4(CH3)4, which exhibits S4 symmetry.
Point Groups and Their Detailed List of Symmetry Elements
| Point group | Order of group, h | Type of symmetry elements |
|---|---|---|
| C1 | 1 | E (=C1) |
| Ci | 2 | E, I (=S2) |
| Cs | 2 | E, σ |
| Cn - groups: (h = n) | ||
| C2 | 2 | E, C2 |
| C3 | 3 | E, C31, C32 |
| C4 | 4 | E, C41, C42 (=C2), C43 |
| C5 | 5 | E, C41, C42, C43, C44 |
| Cnv - groups: (h = 2n) | ||
| C2v | 4 | E, C2, σ |
| C3v | 6 | E, C31, C32, 3σv |
| C4v | 8 | E, C41, C42(=C2), C43, 2σv, 2σv' |
| Cnh - groups: (h = 2n) | ||
| C2h | 4 | E, C2, i=(S2), σh |
| C3h | 6 | E, C31, C32, S31, S35, σh |
| C4h | 8 | E, C41, C42(=C2), C43, S41, S43, σh, i=(S2) |
| Dn - groups: (h = 2n) | ||
| D2 | 4 | E, C2, C2' |
| D3 | 6 | E, C31, C32, 3C2 |
| D4 | 8 | E, 2C4, C2, 4C2 |
| Dnh - groups: (h = 4n) | ||
| D2h | 8 | E, C2, 2C2', i=(S2), σh, 2σv |
| D3h | 12 | E, 2C3, 3C2, σh, 3σv, 2S3, (S31, S35) |
| D4h | 16 | E, 2C4, (C41, C42), C2=(C42), 2C2', 2C2", σh, 2σv, 3σd, i, 2S4 (S41, S43) |
| Dnd - groups: (h = 4n) | ||
| D2d | 8 | E, C2, 2C2', 2σd, 2S4 |
| D3d | 12 | E, 2C3 (C31, C32), 3C2, i, 3σd, 2S6(S61, S63) |
| D4d | 16 | E, 2C4, (C41, C43), C2=(C42), 4C2', 4σd, 4S8(S81, S83, S85, S87) |
| Sn (n=even) - groups: (h = n) | ||
| S4 | 4 | E, S41, S43, C2 |
| S6 | 6 | E, S61, S45, C31, C32, i |
| S8 | 8 | E, S8, S81, S83, S85, S87, C41, C43, C2=(C42) |
| Infinite-point group (h=∞) | ||
| C∞v | ∞ | E, ∞, C∞, ∞σv |
| D∞v | ∞ | E, ∞, C∞, ∞σv, σh, i |
Molecules of Special Symmetry
This class has two groups of molecules:
- Linear or infinite groups
- Groups which contain multiple higher-order axes
Linear or infinite groups:
In addition to all the linear molecules, circle-shaped and cone-shaped ones also belong to this category. These can be further sub-divided into two groups, C∞v and D∞v groups, the presence or absence of i used to distinguish between these two types of groups.
C∞v point group:
This group can be defined the same way as that of Cnv group, where n is infinity. The C∞ axis lies along the inter-nuclear molecules, and since the molecule is linear the σv planes are infinite in number. The order of this group is h = ∞. All hetero-nuclear molecules, and all unsymmetrically substituted linear polyatomic molecules belong to this point group.
Examples are HX (X = F, Cl, Br, I), CO, NO, CN etc.
D∞v Point Group
This group is an extension of the Dnh group (∞). This group of molecules contains a C∞ axis, an infinite number of C2 axes perpendicular to the C∞ axis, and a σh plane. Consequently, the molecule also possesses an infinite number of σv planes and a center of inversion (i). Thus, all centrosymmetric linear molecules belong to this point group.
Typical examples include homonuclear diatomic molecules such as N2, O2, H2, F2, and Cl2.
Molecules Containing Multiple Higher-Order Axes
This is a special class of molecules which contain more than one type of rotational axes (n ≥ 2) that are neither perpendicular to the principal Cn axis (n-highest), as in Dn and related point groups, nor bear any perpendicular relationship. These high-symmetry molecules have shapes corresponding to the five Platonic solids: tetrahedral, octahedral, cube, dodecahedral, and icosahedral.
Tetrahedral Point Groups
The highest-fold axis in these point groups is the C3 axis, which occurs in multiples. Molecules with only C3 axes and additionally only C2 axes belong to T, a pure rotational point group, since they contain only proper rotational axes. All other types of symmetry elements (σv, i, Sn) are absent in this group.
T: 8C3 (4C31, 4C32), 3C2, E
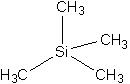
Si(CH3)4
When σd, S4 (collinear with C2 axes) elements are added to the T group elements, we get a full group called Td. The order of this group is 24.
Td: 8C3 (4C31, 4C32), 3C2, E, 6S4 (S41, S43), 6 σd
CCl4
There is another uncommon point group, Th, which can be obtained by adding three planes of symmetry (σh) to the T group. The order of this group is 24.
Th: 8C3 (4C31, 4C32), 3C2, i, 3σh, 8S6 (4S61, 4S65)
Example: Co(NO2)63−
Octahedral Point Groups
This is another class of cubic groups. Additionally, octahedral point groups have multiple C4 axes when compared to that of tetrahedral groups.
When the group contains only rotational axes, it is labelled as the O group. The order (h) of this group is 24.
O: E, 6C4 (3C41, 3C42), 8C3 (4C31, 4C32), 6C2, 3C2′ = 3C42
To the O group elements, if 3σh and 6σd planes are added, a group of higher symmetry can be generated. The order of this group is 48.
Oh: E, 6C4 (3C41, 3C42), 3C2′ = 3C42, 6C2, 8C3 (4C31, 4C32), i, 3σh, 6σd, 6S4 (S41, S43), 8S6 (4S61, 4S65)
Cubane
Icosahedral Groups:
This group contains molecules with either icosahedral or pentagonal dodecahedral shapes and belongs to Ih point groups. The molecules containing only the rotational elements are said to belong to the I point group. The order of this point group is 60, whereas the full group is 120.
I: E, 24C5 (6C51, 6C52, 6C53, 6C54), 20C3 (10C31, 10C32), 15C2
Ih: E, 24C5, 20C3, 15C2, 24S10 (6S101, 6S103, 6S107, 6S109), 20S6 (10S61, 10S65), i, 15σ
Fullerene
Great Orthogonality Theorem:
The matrices of the different Irreducible Representations (IR) possess certain well-defined interrelationships and properties. Orthogonality theorem is concerned with the elements of the matrices which constitute the IR of a group.
The mathematical statement of this theorem is,
Where,
- i, j – Irreducible Representations
- li, lj – Its dimensions
- h – Order of a group
- Γi(R)mn – Element of mth row, nth column of the ith representation
- Γj(R)'m'n' – Element of m′th row, n′th column of the j′th representation
- δij, δmm′, δnn′ – Kronecker delta
Kronecker delta can have values 0 and 1. Depending on that, the main theorem can be expressed as three similar equations:
i.e.,
-
When Γi ≠ Γj and j ≠ i, then δij = 0
Therefore,
ΣR [ Γi(R)mn ] [ Γj(R)'m'n' ]* = 0 -
When Γi = Γj and j = i, then δij = 1
Therefore,
ΣR [ Γi(R)mn ] [ Γi(R)'m'n' ]* = 0
From these two equations, we can state the Orthogonality Theorem as: “The sum of the product of the irreducible representations is equal to zero.” -
When i = j, m = m′, n = n′
Then,
ΣR [ Γi(R)mn ] [ Γi(R)mn ]* =
From the above equations some important rules of the irreducible representations of a group and there character were obtained.
Five Rules Obtained:
-
The sum of the squares of the dimensions of the representations equals the order (h) of the group.
i.e., Σli2 = l12 + l22 + l32 + …… + ln2 = h
Γi(E) – the character of the identity operation E in the ith irreducible representation, which equals the dimension of the representation.
i.e., Σi [Γi(E)]2 = h -
The sum of the squares of the characters in any irreducible representation is equal to h.
i.e., ΣR [Γi(R)]2 = h -
The vectors whose components are the characters of two different irreducible representations are orthogonal.
i.e., ΣR Γi(R) · Γj(R) = 0 when i ≠ j -
In a given representation (reducible or irreducible), the characters of all matrices corresponding to operations in the same class are identical.
Example: In the C3v point group, the operations E, 2C3, and 3σv belong to different classes. The characters of operations in the same class are identical for a particular irreducible representation. - The number of irreducible representations in a group equals the number of classes in the group.
Applications:
Applying these 5 rules we can develop the character table for various point groups. For most chemical applications, it is sufficient to know only the characters of the each of the symmetry classes of a group.
Steps for the Construction of a Character Table:
- Write down all the symmetry operations of the point group and group them into classes.
- Note that the number of irreducible representations (IRs) is determined using the group theory theorem.
- Carefully follow the interrelationships of various group operations.
- Use the orthogonality and normality theorems to fix the characters.
- Generate a representation using basic vectors. Try using basis vectors such as X, Y, Z, Rx, Ry, Rz, etc., and check their transformation properties.
Character Table for C2v Point Group:
1. For the C2v point group, there are 4 symmetry operations:
- E (Identity)
- C2z (180° rotation about the z-axis)
- σxz (reflection in the xz-plane)
- σyz (reflection in the yz-plane)
These operations form 4 classes. The corresponding irreducible representations are denoted as Γ1, Γ2, Γ3, and Γ4.
The character under the identity operation E for each representation is represented as l1, l2, l3, l4.
| C2v | E | C2z | σxz | σyz |
|---|---|---|---|---|
| Γ1 | l1 | |||
| Γ2 | l2 | |||
| Γ3 | l3 | |||
| Γ4 | l4 |
2. The sum of the squares of the dimensions of the symmetry operations = 4.
i.e., l12 + l22 + l32 + l42 = h = 4.
This can only be satisfied by four one dimensional representations.
| C2v | E | C2z | σxz | σyz |
|---|---|---|---|---|
| Γ1 | 1 | |||
| Γ2 | 1 | |||
| Γ3 | 1 | |||
| Γ4 | 1 |
The unknowns for Γ1 is a1, b1, c1, for Γ2 is a2, b2, c2.
| C2v | E | C2z | σxz | σyz |
|---|---|---|---|---|
| Γ1 | 1 | a1 | b1 | c1 |
| Γ2 | 1 | a2 | b2 | c2 |
| Γ3 | 1 | a3 | b3 | c3 |
| Γ4 | 1 | a4 | b4 | c4 |
3. Sum of the squares of the characters of any IR is equal to the order of the group.
i.e., 12 + a12 + b12 + c12 = 4.
| C2v | E | C2z | σxz | σyz |
|---|---|---|---|---|
| Γ1 | 1 | 1 | 1 | 1 |
| Γ2 | 1 | a2 | b2 | c2 |
| Γ3 | 1 | a3 | b3 | c3 |
| Γ4 | 1 | a4 | b4 | c4 |
4. The orthogonality theorem must be satisfied by all the symmetry operations.
i.e., ΣR Γi(R) Γj(R) = 0
i.e., for Γ1 · Γ2
i.e., 1·1 + a1·1 + b2·1 + c2·1 = 0
Let a2 = 1, b2 = -1, and c2 = -1
Then Γ1 · Γ2 = 0
| C2v | E | C2z | σxz | σyz |
|---|---|---|---|---|
| Γ1 | 1 | 1 | 1 | 1 |
| Γ2 | 1 | 1 | -1 | -1 |
| Γ3 | 1 | a3 | b3 | c3 |
| Γ4 | 1 | a4 | b4 | c4 |
For Γ3 · Γ1
i.e., 1·1 + a3·1 + b3·1 + c3·1 = 0
Let a3 = -1, b3 = 1, and c3 = -1
Then Γ1 · Γ3 = 0
| C2v | E | C2z | σxz | σyz |
|---|---|---|---|---|
| Γ1 | 1 | 1 | 1 | 1 |
| Γ2 | 1 | 1 | -1 | -1 |
| Γ3 | 1 | -1 | 1 | -1 |
| Γ4 | 1 | a4 | b4 | c4 |
For Γ4 · Γ1
i.e., 1·1 + a4·1 + b4·1 + c4·1 = 0
Let a4 = -1, b4 = -1, and c4 = 1
Then Γ1 · Γ4 = 0
| C2v | E | C2z | σxz | σyz |
|---|---|---|---|---|
| Γ1 | 1 | 1 | 1 | 1 |
| Γ2 | 1 | 1 | -1 | -1 |
| Γ3 | 1 | -1 | 1 | -1 |
| Γ4 | 1 | -1 | -1 | 1 |
Rules For Assigning Mullicon Symbols:
-
If the IR is unidimensional term A or B is used.
If it is two dimensional E is used.
If it is three dimensional T is used. - If one dimensional IR is symmetric with respect to the principle axis Cn, i.e., character of Cn is +1, the term A is used. If it is -1, the term B is used.
- If IR is symmetric with respect to subsidiary axes then subscript 1 is given and is antisymmetric then subscript 2 is given.
- Prime (′) and double prime (″) marks are used for indicating symmetric or antisymmetric with respect to horizontal plane.
- ‘g’ and ‘u’ subscripts are given for those which are symmetric and antisymmetric respectively with respect to centre of symmetry.
| C2v | E | C2z | σxz | σyz |
|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 |
| A2 | 1 | 1 | -1 | -1 |
| B3 | 1 | -1 | 1 | -1 |
| B4 | 1 | -1 | 1 | -1 |
In any character table there are 4 different areas.
- Area I – Characters of symmetry operations
- Area II – Mullicon Symbols
- Area III – Cartesian coordinates of rotation axes
- Area IV – Binary Products
Area III:
In order to assign the Cartesian coordinates, different operations are performed on each of the axes. Here we find the symbols X, Y, Z represent coordinates and rotations Rx, Ry, and Rz.
Consider a vector along the Z axis. The identity operation does not change the direction of the head of the vector. On performing C2, σxz, and σyz operations, no change occurs. Hence, its characters are 1 1 1 1. Therefore, the vector 'Z' transforms under A1.
The characters are 1 -1 1 -1 corresponding to B1. And with respect to vector Y, the characters are 1 -1 -1 1 and therefore correspond to B2.
A similar arrangement can be made for the rotation axes Rx, Ry, and Rz, representing rotation about the X, Y, and Z axes, respectively.
To determine how they transform, a curved arrow should be considered around the respective axes. If the direction of the head of the curved arrow does not change due to the symmetry operation, the character is +1; otherwise, it is -1.
The characters are 1 1 -1 -1. Therefore, it corresponds to A2 and it becomes Rz.
The characters are 1 -1 1 -1. Therefore it will be B1 and it becomes Rx. Similarly B2 becomes Ry.
Therefore,
| C2v | E | C2z | σxz | σyz | Linear Functions, Rotations |
|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | Z |
| A2 | 1 | 1 | -1 | -1 | Rz |
| B1 | 1 | -1 | 1 | -1 | X, Ry |
| B2 | 1 | -1 | -1 | 1 | Y, Rx |
Area IV:
Which represents the squares and binary products.
A1 = Z = 1 1 1 1
A1² = Z² = 1 1 1 1 = A1
B1 = X = 1 -1 1 -1
B1² = X² = 1 1 1 1 = A1
B2 = Y = 1 -1 -1 1
B2² = Y² = 1 1 1 1 = A1
XY = B1 · B2 = 1 1 -1 -1 = A2
XZ = B1 · A1 = 1 -1 1 -1 = B1
YZ = B2 · A1 = 1 -1 -1 1 = B2
Therefore the actual character table for C2v point group will be:
| C2v | E | C2z | σxz | σyz | Linear Functions, Rotations | Quadratic |
|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | Z | X², Y², Z² |
| A2 | 1 | 1 | -1 | -1 | Rz | XY |
| B1 | 1 | -1 | 1 | -1 | X, Ry | XZ |
| B2 | 1 | -1 | -1 | 1 | Y, Rx | YZ |
Character Table for C3v Point Group:
- For C3v point group, there are 6 symmetry operations and 3 classes, i.e., Γ1, Γ2, Γ3.
- The sum of the squares of the dimensions of the symmetry operations = 6.
i.e., l12 + l22 + l32 = h = 6.
This can only be satisfied by, 2 one-dimensional and 1 two-dimensional representations.
| C3v | E | 2C3 | 3σv |
|---|---|---|---|
| Γ1 | 1 | a₁ | b₁ |
| Γ2 | 1 | a₂ | b₂ |
| Γ3 | 2 | a₃ | b₃ |
- The sum of the dimensions of Γ1 is also 6.
Therefore, its characters are (1 1 1).
| C3v | E | 2C3 | 3σv |
|---|---|---|---|
| Γ1 | 1 | 1 | 1 |
| Γ2 | 1 | a₂ | b₂ |
| Γ3 | 2 | a₃ | b₃ |
- All operations must satisfy the orthogonality condition,
ΣR Γi(R) · Γj(R) = 0
i.e., for Γ1 · Γ2:
1·1 + 2·a2·1 + 3·b2·1 = 0
Let a2 = 1 and b2 = −1
Then Γ1 · Γ2 = 0
| C3v | E | 2C3 | 3σv |
|---|---|---|---|
| Γ1 | 1 | 1 | 1 |
| Γ2 | 1 | 1 | −1 |
| Γ3 | 2 | a₃ | b₃ |
i.e., For Γ3 · Γ2:
2·1 + 2·a3·1 − 3·b3·1 = 0
Let a3 = −1 and b3 = 0
Then Γ3 · Γ2 = 0
| C3v | E | 2C3 | 3σv |
|---|---|---|---|
| Γ1 | 1 | 1 | 1 |
| Γ2 | 1 | 1 | −1 |
| Γ3 | 2 | −1 | 0 |
For any character table, there are four areas.
For Area I:
Assign the Mulliken symbols.
| C3v | E | 2C3 | 3σv |
|---|---|---|---|
| A1 | 1 | 1 | 1 |
| A2 | 1 | 1 | −1 |
| E | 2 | −1 | 0 |
For Area III:
In order to assign the Cartesian coordinates, different operations are performed on each of the axes. Here we were finding the symbols X, Y, Z represent coordinates and rotations Rx, Ry and Rz.
Consider,
The characters are 1 1 1 corresponding to A1.
The characters are 1 −1 1, the character corresponding to C3 will be −1. Therefore, it will be E.
Similarly, for vector Y, we get 1 −1 1 and this is also E.
Similar arrangements could be made for the rotation axes Rx, Ry, and Rz.
The characters are 1 −1 1. Therefore, it corresponds to E and it will become Rx.
The characters are 1 1 −1. Therefore, it corresponds to A2 and it will become Rz.
Similarly, for E the characters are 2 −1 0 and it will become Ry.
| C3v | E | 2C3 | 3σv | Linear Functions, Rotations |
|---|---|---|---|---|
| A1 | 1 | 1 | 1 | Z |
| A2 | 1 | 1 | −1 | Rz |
| E | 2 | −1 | 0 | (X, Y), (Rx, Ry) |
Area IV:
Which represents the squares and binary products.
A1 = Z = 1 1 1
A12 = Z2 = 1 1 1 = A1
XY = E = 2 −1 0 = E
XZ = E · A1 = 2 −1 0 = E
YZ = E · A1 = 2 −1 0 = E
Therefore the actual character table for C3v point group will be,
| C3v | E | 2C3 | 3σv | Linear Functions, Rotations | Quadratic |
|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | Z | Z2 |
| A2 | 1 | 1 | −1 | Rz | |
| E | 2 | −1 | 0 | (X, Y), (Rx, Ry) | (XY), (XZ), (YZ) |
Some Important Character Tables for Molecular Point Groups:
- Character Table for Non-Axial Point Groups
- Character Table for Cn Point Groups
- Character Table for Cnv Point Groups
- Character Table for Cnh Point Groups
- Character Table for Dn Point Groups
- Character Table for Dnh Point Groups
- Character Table for Dnd Point Groups
- Character Table for Sn Point Groups
- Character Tables for Higher Point Groups
- Character Tables for Linear Point Groups
