Procedure

(a) Experimental Set up and Procedure

You see a physical model of a Spring-Mass-Damper system, supported at bottom (Spring and damper grounded and supporting a mass). Values of mass, spring stiffness, and damping coefficient are entered in the windows provided for the purpose. A vertical force whose magnitude varies sinusoidaly with respect to time is applied on the mass i.e. a harmonic excitation is given to the system acting on the mass. The amplitude of the force is entered. The range of frequencies of the harmonic force is prescribed by entering the lowest and highest values of the range of frequencies. The frequency is increased in steps, dwelling at each frequency for some time and reaching the highest frequency of the range. An accelerometer is shown mounted on the mass to measure its acceleration and in turn its displacement. Output of the accelerometer goes to vibration analyzer displaying displacement (twice integrated from acceleration) versus time. By clicking the button 'start', the harmonic force starts acting on the mass. The plot of amplitude of vibration of the mass, X v/s ω, and its phase difference with respect to the excitation-force can is seen in the windows. The mass can be seen vibrating. Observation of the plot are made and analyzed later. Results will be tallied with some numerical calculations. The set of observations will be made for different dampers, i.e. for different values of damping factor, ζ.

(b) Observation and analysis:

1. Observe the plot X v/s ω (or X/X0 v/s ω/ωn). Note that X increases gradually till it reaches a certain value of ω and then decreases. Values of X are smaller for greater ζ (or C) and also the peak occurs at slightly changed ω

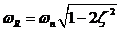
2. Compare the plots for different values of damping factors and note the reduced response and slight change in resonance frequency. Hence note that resonance is damping-controlled and amplitude of vibration can be considerably reduced by damping.

3. Use the values of frequency of resonance, ωR, and damping factor, ζ, to find ωn from 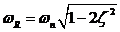Tally the value so obtained with the value obtained from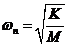

(c) Try this and observe what happens and why

1. Compare the plots obtained through the experiments with the plots given in the books on Mechanical Vibration.

2. How does an over-damped system respond to a harmonic excitation, i.e. the value of damping coefficient C is greater than CC, or the value of ζ is greater than 1.? Refer to the text. Record/Comment yourself on the observations