Theory:A first order system is one in which highest power of ‘s’ in denominator if transfer function defines order of the system.
For first order system, $${\frac{C(s)}{R(s)}=\frac{1}{sT+1}}$$ ...... (1),
$${C(s)=\frac{1}{sT+1}R(s)}$$

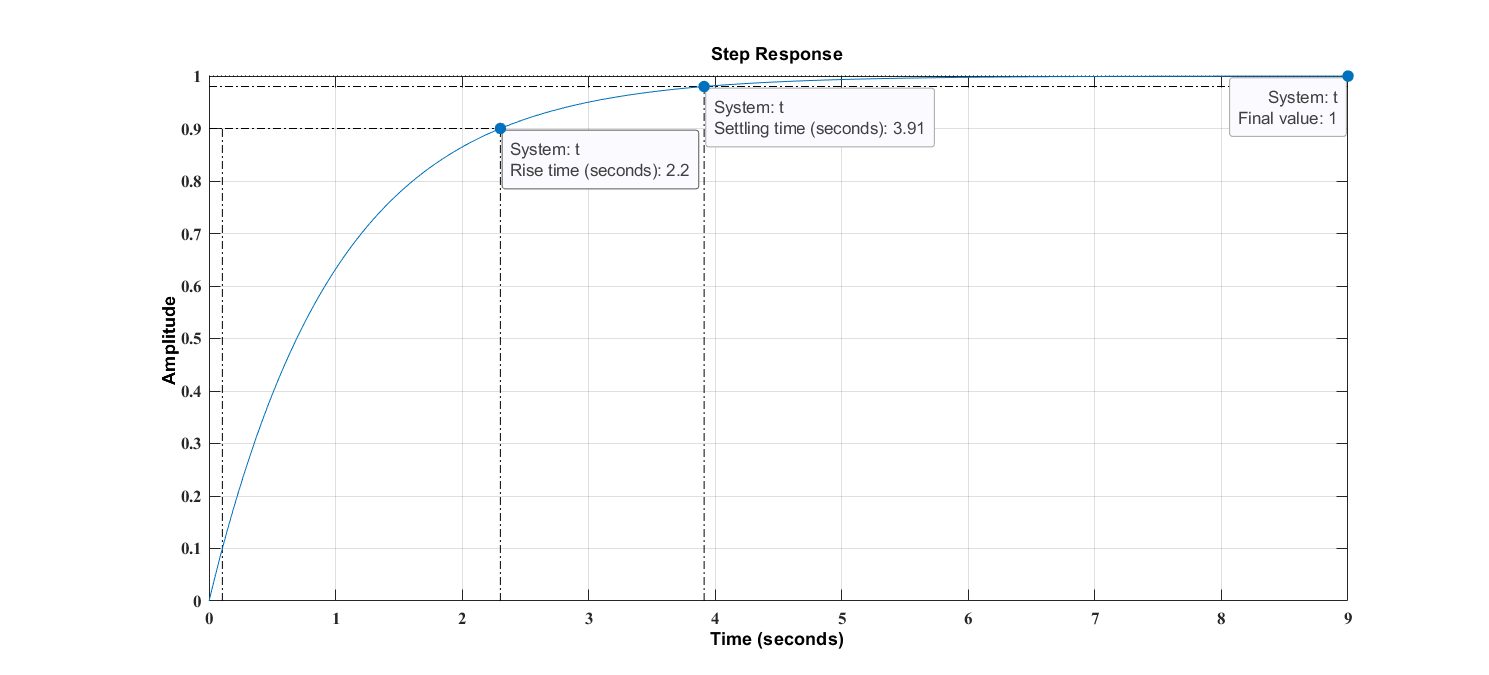
1. For the unit-step input:

R(t)=1,
R(s)=1/s (a),
Since the Laplace transform of the unit step function is 1/s , substituting R(s)=1/s in equation (1), $${C(s)=\frac{1}{sT+1} * \frac{1}{s}}$$ Substitute the value of R(s)
Expanding C(s) into partial fractions gives, $${C(s)=\frac{1}{s}-\frac{T}{sT+1}}$$...... (2),
$${C(s)=\frac{1}{s}-\frac{1}{s+(\frac{1}{T})}}$$ Taking the inverse Laplace t+-ransform of equation (2),we get,
C(t) = 1- e^-t/T for t ≥ 0 ...... (3),
Equation (3) shows that initially (when t=0), the output C(t) is zero and finally (t→∞) e^-t/T is zero and the output C(t) becomes unity.
At t=T,   C(t) = 1 – e^-1 = 1 – 0.368 = 0.632,
That’s , the output response has reached 63.2 % of it’s final value . T is known as the time constant. Thus, the time constant T is defined as the time required for the output response to attain 63.2% of its final value or steady state value.
Equation (3) shows that the response curve is exponential in nature as shown on figure:

2. For the unit-impulse input:

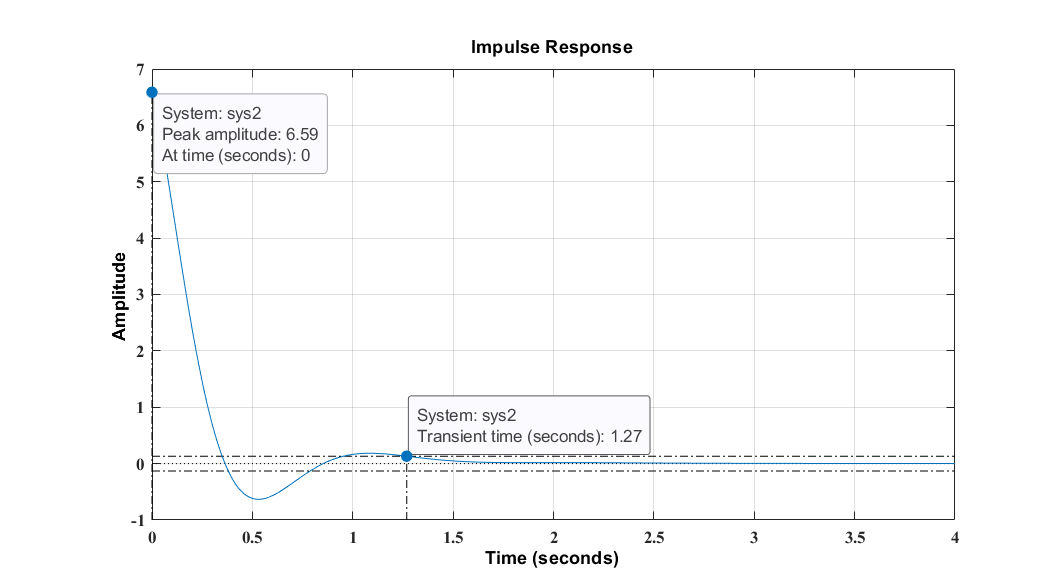
Response of the first order system with unit impulse response:
For the unit-impulse input
R(s) = 1
$${C(s) =\frac{1}{sT+1}R(s)}$$ ...... (1),
Subsituting the value of R(S) = 1 in equation (1), we get
$${C(s) =\frac{1}{sT+1}}$$ $${C(s) =\frac{1}{T}\frac{1}{s+\frac{1}{T}}}$$ ...... (2),
Taking the inverse laplace transform of the equation of (2), we get the output response as $${C(s) = \frac{1}{T}e^\frac{-t}{T}}$$ for t >= 0 ...... (3),
The output response curve is shown below in the figure: