Bravais Lattice

A Bravais lattice is a mathematical construct representing an infinite array of discrete points in three-dimensional space such that the environment around each point is identical. An alternative method to generate Bravais lattice is to start with a single point and consider all points that can be reached by translating this point by integer multiples of three (non-planar) vectors; this infinite set of points is Bravais lattice (with single point basis). A Bravais lattice forms the framework upon which a crystal structure is built. While the lattice itself is an abstract concept (an array of points), a crystal structure is formed by associating a motif (such as an atom, molecule, or group of atoms) with each lattice point.

Mathematical Representation of a Lattice

The position of a lattice point is given by: $$\bar r = n_{1}\bar a_{1} + n_{2}\bar a_{2} + n_{3}\bar a_{3}$$ Where:

• $a_{1}$, $a_{2}$, $a_{3}$ are the primitive vectors which generate the lattice
• $n_{1}$, $n_{2}$, $n_{3}$ are the integers representing the coordinates of the lattice point relative to the origin. These coordinates generate a repeating pattern that extends infinitely in all directions, forming the lattice.

Characteristics of Bravais Lattices

Key characteristics of Bravais lattices:

• Periodicity: Each point has an identical environment, creating a repeating pattern in three dimensions.
• Unit Cell: The smallest building block of a lattice that can generate the entire structure by translation.
• No Physical Atoms: The lattice is an abstract geometric construct; it represents the arrangement of points in space, not atoms.

Types of Bravais Lattices

There are 14 types of Bravais lattices, grouped into seven crystal systems based on symmetry and geometry. Two common examples are:

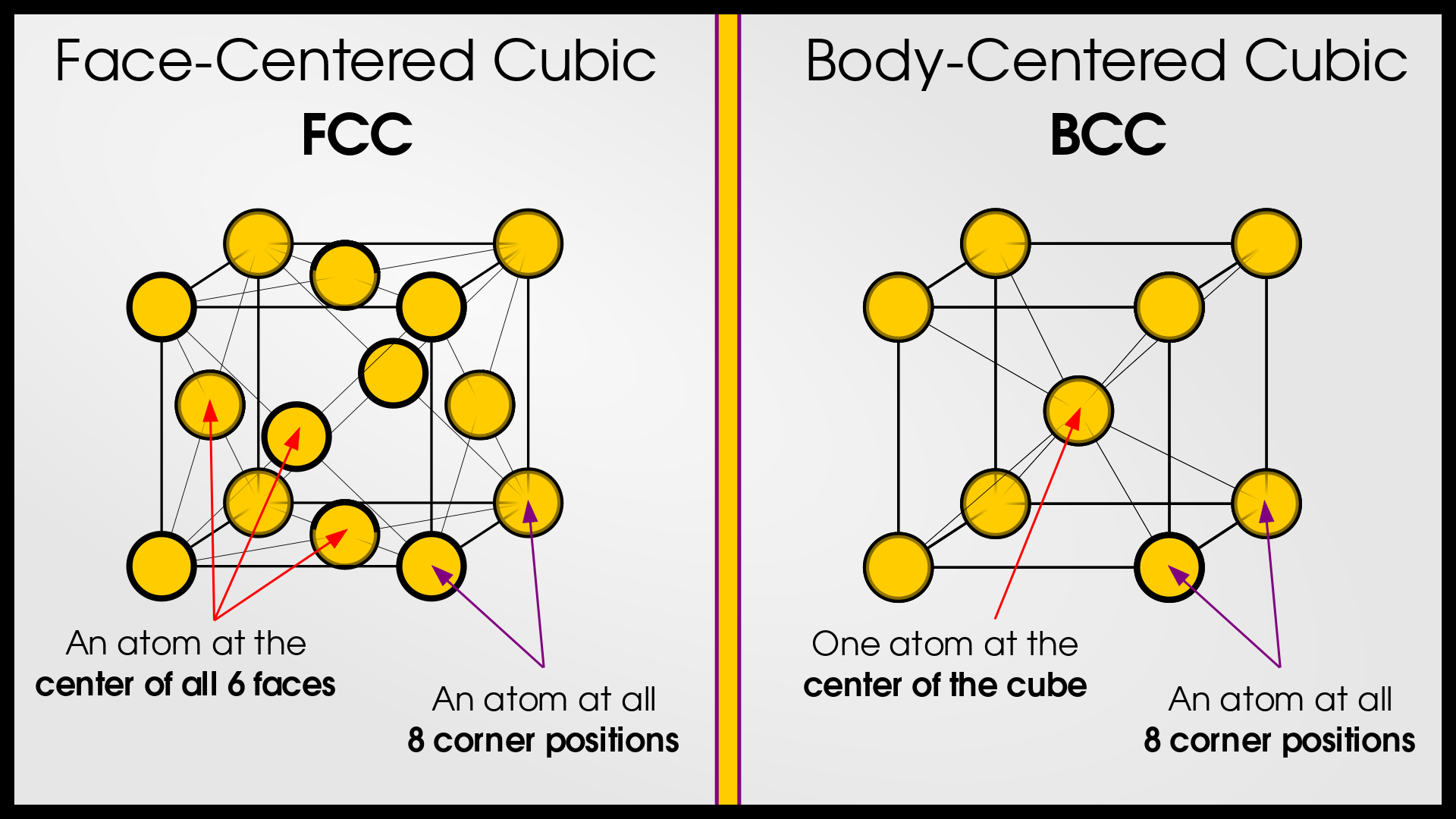
• Face-Centered Cubic (FCC): Lattice points are located at the corners and center of each face of the cube.
• Body-Centered Cubic (BCC): Lattice points are located at the corners and the center of the cube.

For a visual representation, see the diagrams below or explore these structures in the simulation.

How Lattices Form Crystals

To form a crystal, a motif is associated with each lattice point.

• The lattice provides the periodic framework.
• The motif(atoms, molecules, etc.) is repeated at every lattice point. Together, these create the crystal structure, which exhibits periodicity and symmetry. For example, In an FCC lattice, if a single atom is used as the motif, it forms a crystal structure like that of copper.