Theory

The theory associated with Experiment-4 is divided into two parts:

(1) Standard array decoding
(2) Syndrome decoding

1    Standard array decoding

The decoding consists of estimating the transmitted codeword corresponding to the given received vector. Standard array decoding is a method for decoding linear block codes when the noise is introduced by the binary symmetric channel (BSC) with cross-over probability $p$, denoted by BSC $(p)$. For a detailed description of standard array decoding, please refer [1] (Chapter 4, Section 3.5). We shall next briefly discuss how to construct a standard array corresponding to the given linear block code $\mathcal{C}(n,k)$ and then discuss how to decode the given received vector $\mathbf{y} \in \mathbb{F}_2^n$ using it.
Let $\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_{2^k}$ be the set of codewords of the given code $\mathcal{C}(n,k)$. A codeword is chosen randomly and transmitted over the BSC to get the received vector $\mathbf{y} \in \mathbb{F}_2^n$. Note that for the BSC$(p)$, $\mathbf{y}$ can be any vector in $\mathbb{F}_2^n$, irrespective of the transmitted codeword. The core idea of standard array construction consists of dividing all possible $2^n$ vectors into $2^k$ disjoint subsets such that there is exactly one codeword in each subset. Thus the given vector $\mathbf{y}$ can be associated with the unique codeword that lies in the same subset as that of $\mathbf{y}$ and in standard array decoding, $\mathbf{y}$ is decoded to this codeword.

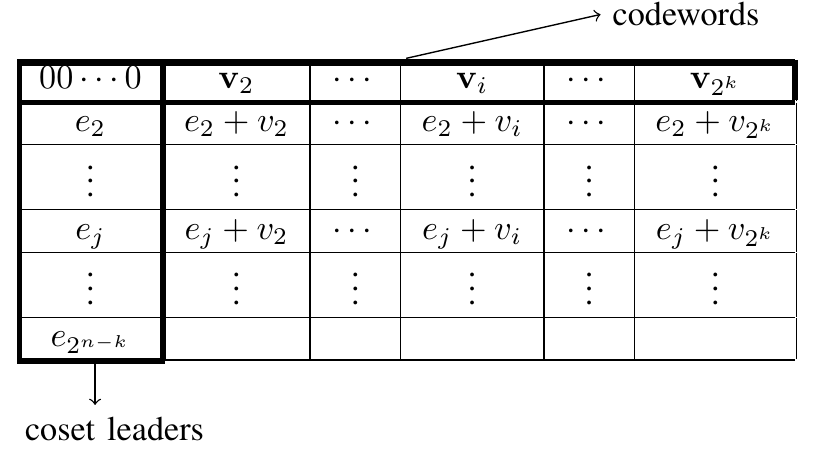
                 Figure 1: A general structure of the standard array

For BSC$(p)$ with $p<1/2$, an optimal way of dividing these $2^n$ vectors into $2^k$ disjoint subsets provides a standard array. A standard array is a table with $2^k$ columns and $2^{n-k}$ rows such that a distinct vector in $\mathbb{F}_2^n$ is placed in each entry of this table. For the given row, the vector in the first column is called as the coset leader of that row.The procedure for constructing a standard array is provided below.

• First row: Put all-zero codeword in the first row and the first column. Thus all-zero vector is the coset leader of the first row. The remaining $2^k-1$ non-zero codewords are placed in the remaining columns of the first row. Without loss of generality, let $\mathbf{v}_1$ be all-zero codeword and $\mathbf{v}_2, \mathbf{v}_3, \ldots, \mathbf{v}_{2^k}$ be the non-zero codewords. Then the first row of the standard is illustrated in Figure 1.

• Rows $2$ to $2^{n-k}$: For the $j$th row, $j = 2, 3, \ldots, 2^{n-k}$, do the following:

  
  - Identify a vector of minimum weight that has not appeared in the rows $1$ to $j-1$. This vector is chosen as the coset leader of the $j$th row. Let $\mathbf{e}_j$ denotes the coset of the $j$th row.
  - The remaining entries in the $j$th row are obtained by adding $\mathbf{e}_j$ to the codeword corresponding to the each column, i.e., the entry in the $i$th column is given by $\mathbf{e}_j + \mathbf{v}_i$, where $i = 2, 3, \ldots, 2^{k}$ (see Figure 1).

Note that the set of coset leaders $\{ \mathbf{e}_2, \mathbf{e}_3, \ldots, \mathbf{e}_{2^{n-k}}\}$ need not be unique. Further, the non-zero codewords $\mathbf{v}_2, \mathbf{v}_3, \ldots, \mathbf{v}_{2^k}$ can be placed in any order in the first row of the standard array. Hence a standard array corresponding to the given code is not unique. Let us consider an example for standard array construction.

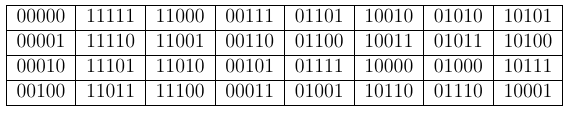
Example   1   Let {00000, 11111, 11000,01010, 10101, 00111, 01101, 10010} be the set of codewords of a linear block code of length $n=5$. Note that the dimension of this code is $k=3$. A standard array corresponding to this code is given in Table 1. It can be verified that this standard array is not unique

         Table  1:  Standard array of a linear block code of length 5

Let us now discuss how to decode the given received vector $\mathbf{y}$ using standard array. This procedure is summarized below.

• Locate $\mathbf{y}$ in the standard array. Suppose $\mathbf{y}$ lies in the $i$th column.
• $\mathbf{y}$ is decoded as $\mathbf{v}_i$, which is the codeword corresponding to the $i$th column.
  

Suppose $\mathbf{v}_i$ is the transmitted codeword and $\mathbf{e}_j$ is the error introduced by the BSC then the received vector will be $\mathbf{y} = \mathbf{v}_i + \mathbf{e}_j$. Observe that we will be able to correct such an error pattern via standard array decoding. It can be shown that the set of $2^{n-k}$ coset leaders are the set of error patterns that can be corrected using standard array decoding.

2    Syndrome decoding

For the given linear block code $\mathcal{C}(n,k)$ with parity check matrix $H$, the syndrome of the given vector $\mathbf{y} \in \mathbb{F}_2^n$ is defined as the vector $\mathbf{s} \in \mathbb{F}_2^{n-k}$ given by

$$\begin{align*} \mathbf{s} \coloneqq \mathbf{y}H^T. \end{align*}$$

Consider the following properties of syndromes (proofs can be found in [1]):

• Property 1: Syndromes of the vectors that lie in the same row of the standard array are the same, i.e., for $\mathbf{y}_{1}$ and $\mathbf{y}_{2}$ that lie in the same row of the standard array we have $$\begin{align*} \mathbf{y}_{1}H^T = \mathbf{y}_{2}H^T. \end{align*}$$
• Property 2: Syndromes of the vectors that lie in different rows of the standard array are different, i.e., for $\mathbf{y}_{1}$ and $\mathbf{y}_{3}$ that lie in different rows of the standard array we have
  $$\begin{align*} \mathbf{y}_{1}H^T \neq \mathbf{y}_{3}H^T. \end{align*}$$
  

Properties 1 and 2 indicate that there are exactly $2^{n-k}$ distinct syndromes and these are the syndromes of the coset leaders. One this needs to only keep a track of the coset leaders and their corresponding syndrome and simplify the standard array decoding procedure as follows.

• For the given received vector $\mathbf{y}$, compute its syndrome $\mathbf{s} = \mathbf{y}H^T$.
• Locate the coset leader whose syndrome is equal to this $\mathbf{s}$, i.e., locate coset leader $\mathbf{e}_l$ such that $\mathbf{e}_jH^T = \mathbf{s}$.
• Decoded codeword is given by $\hat{\mathbf{v}} = \mathbf{y} + \mathbf{e}_j$.

It can be verified that the standard array and syndrome decoding are equivalent and would decode the given $\mathbf{y}$ to the same codeword. The advantage of syndrome decoding is that storage space required is less as compared with standard array decoding.