Effect of load on wear of materials
The applied load directly influences the wear rate, and it can typically be measured using an empirical relationship known as Archard's wear equation, which is given below.

Where, Q is the wear rate [mm3/N·m] of soft material, W is the applied load (N), and L is the sliding distance (m). K is the material specific constant known as the wear coefficient which also depends on the operating wear mechanism.
Archard's wear equation can be modified to incorporate additional variables, such as material hardness (H, measured in GPa). The modified equation is known as Archard's wear equation and is expressed as follows.
Thus, Q amounts for the total volume of wear debris of soft material produced. Archard's wear equation assumes that all asperities present on sliding tribosurfaces result in material removal. In the modified Archard wear equation, the coefficient of wear is dimensionless.
Even Archard's wear equation is empirical, and while it can shed light on the impact of load on wear rate, it also relies on several other variables, including load conditions and operating wear mechanisms.
Effect of load on stress distribution
Stress distribution can be significantly affected by the nature of the applied load. If the load is evenly distributed, it can help promote uniform wear and prevent localized high-stress areas that could accelerate wear. However, if the load distribution is uneven, it can lead to concentrated stresses and localized wear.
Effect of load on wear mechanisms:
Adhesive wear occurs when two surfaces come into contact and adhere to each other, resulting in material transfer and subsequent wear. Higher loads can increase the contact pressure between surfaces, promoting adhesion and potentially increasing adhesive wear.
When hard particles or asperities causes wear down the surface of a substance, results in an abrasive wear. In some circumstances, a greater load can assist in deeply enmeshing abrasive particles into the material, limiting their capacity to induce additional wear. However, at excessively high loads, abrasive particles can cause severe damage to the material.
According to equation 1, a material has a larger propensity for wear if its wear coefficient (K) is higher, which means that the material will wear out faster under a specific set of circumstances. The wear coefficient depends on materials and wear mechanisms. Here are some approximate ranges of wear coefficients (in mm3/ N·m) for common materials and wear mechanisms:
Effect of load on fatigue wear:
Fatigue wear is caused by repeated cyclic loading, which can lead to the formation and propagation of cracks in the material. Higher loads can accelerate fatigue wear, as they impose greater stress amplitudes on the material, reducing its fatigue life.
Effect of load on lubrication film thickness:
The presence of lubrication between surfaces can significantly influence wear behavior. Under higher loads, the lubricant film thickness may decrease, leading to increased metal-to-metal contact and higher wear rates. Adequate lubrication is crucial to minimize wear, especially under heavy loads. Typically, to avoid wear the lubrication film thickness must be proportional to the applied load. In an elastohydrodynamic lubrication (EHL), the lubrication film thickness (h) must cope the applied load (W) and sliding velocity (V) and be calculated using the Dowson-Higginson equation as follows:
Typically, the effect of load on the wear rate is graphically represented in wear maps with other parameters such as sliding speed and material properties. These maps are constructed by conducting experiments under various combinations of parameters and plotting the resulting wear rates. They provide a more comprehensive understanding of wear behavior and can help identify optimal operating conditions to minimize wear.
Tribo-couple for the test
Stainless steel flat and ball

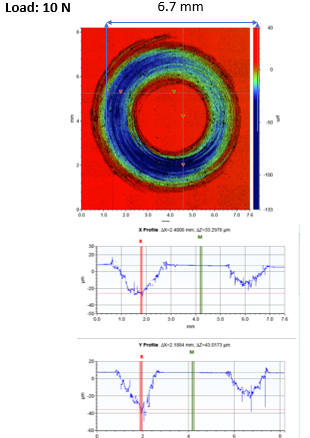
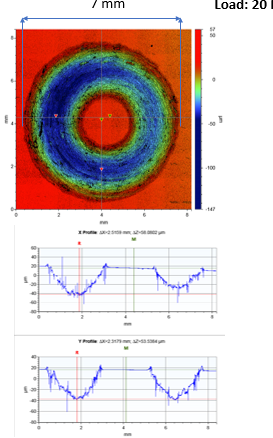
Results
Test 1
Sample: 316 L
stainless steel (Ra= 16 nm)
Counter body: stainless steel
Load: 10N
Speed: 50 RPM
Time: 30 min
Test 2
Sample: 316 L
stainless steel (Ra= 28 nm)
Counter body: stainless steel
Load: 20N
Speed: 50 RPM
Time: 30 min
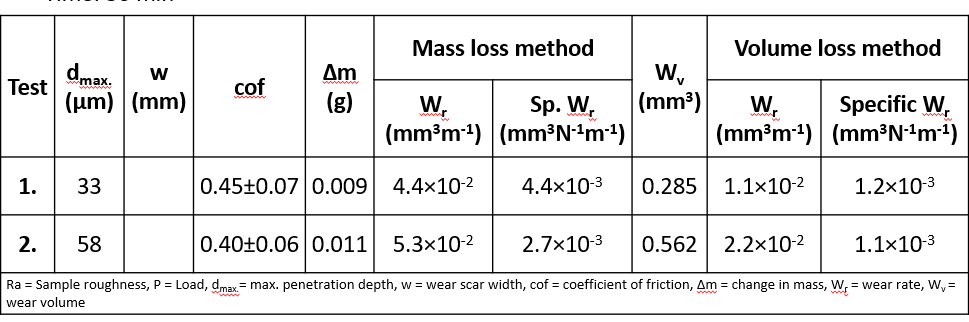
Wear scar depth and wear scar width increase with increase in load
Wear rate increases with increase in load
Specific wear rate does not vary with load
In general, the coefficient of friction for metallic pairs tends to increase under low loads as the load rises, due to the breakdown of the oxide film and/or elastic deformation.
It remains at a high value for a load range and begins to drop at high loads
because of interfacial changes caused by wear
