Disc Type Flywheel
INTRODUCTION
User Objectives and Goals:
- To explain the structure of a disc type flywheel
- To examine the time taken for the metal bob to reach the ground by varying the radius and mass, and applying the angular acceleration equation and equation of motion to calculate the time in which mass will descend
- To analyse the time required for the metal bob to touch the ground for rim type and disc type flywheel.
- To compare the application of rim type flywheel over disc type flywheel.
Theory
A flywheel is an inertial energy storage device which is designed to store rotational energy efficiently. By absorbing mechanical energy it serves as a reservoir i.e. storing energy when the supply of energy is more than what is required and releasing it during the period when the requirement of energy falls short. A flywheel is a spinning wheel or disc with a fixed axle so that rotation is only about one axis.
Due to moment of inertia, flywheels resist changes in rotational speed. The amount of energy stored in a flywheel is proportional to the square of its rotational speed.
The single cylinder engine is a prime candidate for the use of a flywheel. The intermittent nature of its power stroke makes it necessary to store kinetic energy, to carry the piston through the Otto cycle’s exhaust, intake, and compression stroke during which work must be done in the system.[1]
An important application of a flywheel is in a mechanical press where for a fraction of time high energy is required for actual punching, shearing or forming. This energy is supplied by the flywheel. During the longer non active period, the speed of the flywheel is built up slowly by a low powered motor. Thus, the motor is not overloaded and also results in energy saving. [2]
In Rim type of flywheel, the mass of the flywheel is concentrated at the rim only i.e. not throughout the radius but only at the radius which is just opposite to disc type, thus imparting higher moment of inertia than disc type.
Equations/formulas:
In this experiment, the potential energy of mass m is converted into its translation kinetic energy, rotational kinetic energy of flywheel and some of the energy is lost in overcoming frictional force. The equation of conservation of energy at the instant when the mass touches the ground can be written as
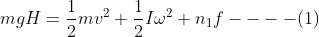
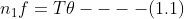
Here 
is the velocity of mass and 
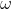is the angular velocity of flywheel at the instant when the mass touches the ground. Here 
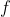is the frictional energy lost per unit rotation of the flywheel and it is assumed to be steady. 
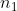is the number of rotations completed by the flywheel, when the mass attached to the string has left the axle.
Even after the string has left the axle, the fly wheel will continue to rotate and its angular velocity decreases gradually and will come to rest when all the rotational kinetic energy has been used up by the frictional energy. If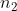 
is the number of rotations made by the flywheel after the string has left the axle,
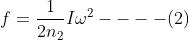
Now, substituting equation (2) in equation (1)
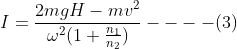
The expression for the moment of inertia can be written as equation (4) by taking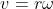 
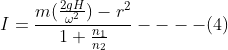
Where,
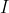is the mass moment of Inertia of Disc=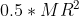 
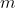is mass
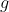is acceleration of gravity
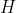is height
is the velocity of mass
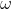is the angular velocity
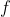is the frictional energy lost per unit rotation
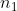is the number of rotations completed by the flywheel
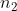the number of rotations made by the flywheel after the string has left the axle [3]
