For a very brief theory of digital signature schemes and their analysis, click here

Digital signatures are cryptographic mechanisms that provide authentication, integrity, and non-repudiation for digital documents and messages. Unlike handwritten signatures, digital signatures use mathematical algorithms to ensure that a document hasn't been altered and to verify the identity of the signer.

How Digital Signatures Work

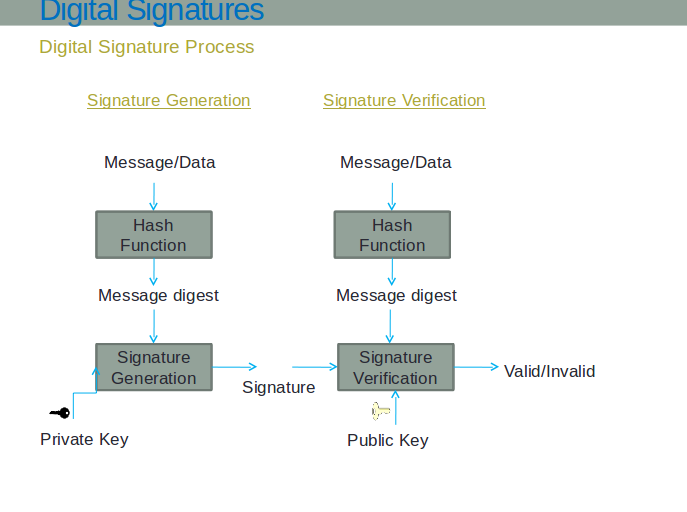
The digital signature process involves three main phases:

1. Hash Generation: $$h = H(m)$$ The original message $m$ is processed through a cryptographic hash function $H$ (such as SHA-256) to create a fixed-size digest $h$.

2. Signature Creation: $$s = \text{Sign}_{sk}(h) = h^d \bmod n$$ The hash $h$ is encrypted using the signer's private key $d$ to create the digital signature $s$.

3. Verification:

$$\text{Verify}_{pk}(m, s) = \begin{cases} \text{Valid} & \text{if } H(m) = s^e \bmod n \\ \text{Invalid} & \text{otherwise} \end{cases}$$

Recipients can verify the signature using the signer's public key $e$ to decrypt the signature and compare it with a freshly computed hash.

RSA-Based Digital Signatures

RSA (Rivest-Shamir-Adleman) is widely used for digital signatures due to its mathematical foundation:

Key Properties:

• Key Generation: Create a public-private key pair $(e, n)$ and $(d, n)$
• Signing: Encrypt the message hash with the private key: $s = H(m)^d \bmod n$
• Verification: Decrypt the signature with the public key: $H(m) \stackrel{?}{=} s^e \bmod n$

RSA Security Assumption: The security of RSA digital signatures relies on the difficulty of the Integer Factorization Problem: $$\text{Given } n = p \times q \text{, find } p \text{ and } q$$

Trapdoor Function: RSA uses a trapdoor one-way function where:

• Easy direction: Computing $y = x^e \bmod n$ is efficient
• Hard direction: Computing $x = y^d \bmod n$ without knowing $d$ is computationally infeasible

Mathematical Representation

For RSA digital signatures:

Signature Generation: $$s = H(m)^d \bmod n$$

Signature Verification: $$H(m) = s^e \bmod n$$

Where:

• $H(m)$ is the hash of message $m$
• $d$ is the private key exponent
• $e$ is the public key exponent
• $n$ is the modulus ($n = p \times q$ for primes $p$ and $q$)

RSA Key Generation Process:

1. Choose two large prime numbers $p$ and $q$
2. Compute $n = p \times q$
3. Compute Euler's totient function: $\phi(n) = (p-1)(q-1)$
4. Choose public exponent $e$ such that $1 < e < \phi(n)$ and $\gcd(e, \phi(n)) = 1$
5. Compute private exponent $d$ such that $d \equiv e^{-1} \pmod{\phi(n)}$

Digital Signature Algorithm Steps:

Signing Process:

1. Compute message hash: $h = H(m)$
2. Generate signature: $s = h^d \bmod n$
3. Send $(m, s)$ to verifier

Verification Process:

1. Compute message hash: $h' = H(m)$
2. Decrypt signature: $h'' = s^e \bmod n$
3. Verify: signature is valid if $h' = h''$

Security Properties

Digital signatures provide three key security properties:

1. Authentication: Verifies the identity of the message sender
2. Integrity: Ensures the message hasn't been modified
3. Non-repudiation: Prevents the sender from denying they signed the message

Key Size Considerations

The security of RSA digital signatures depends on key size and computational complexity:

Key Size	Security Level	Factorization Complexity	Use Case
512-bit	$\approx 2^{86}$ operations	Vulnerable to modern attacks	Educational only
1024-bit	$\approx 2^{103}$ operations	Moderate security	Legacy systems
2048-bit	$\approx 2^{112}$ operations	Currently recommended minimum	Production use
4096-bit	$\approx 2^{140}$ operations	High security	High-value applications

Security Growth: The security of an $n$-bit RSA key against factorization attacks is approximately: $$\text{Security} \approx 2^{\frac{1.9 \times (\log_2 n)^{1/3} \times (\log \log_2 n)^{2/3}}{3}}$$

Performance vs Security Trade-off:

• Signature time: $O((\log n)^3)$ for $n$-bit keys
• Verification time: Typically faster due to small public exponent $e$ (often $e = 65537 = 2^{16} + 1$)
• Key generation time: Increases significantly with key size due to primality testing