Depth First Search
Differences between BFS and DFS
Key differences between BFS and DFS
- BFS is a vertex-based algorithm while DFS is an edge-based algorithm.
- Queue data structure is used in BFS. On the other hand, DFS uses stack or recursion.
- Memory space is efficiently utilized in DFS while space utilization in BFS is not effective.
- BFS is an optimal algorithm while DFS is not optimal.
- DFS constructs narrow and long trees whereas BFS constructs wide and short trees.
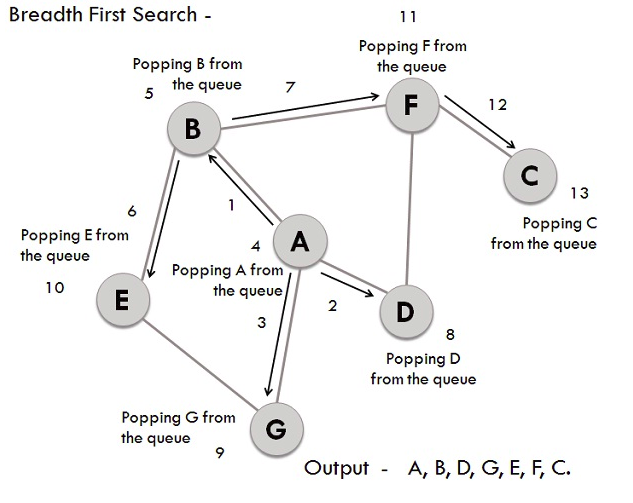
BFS traversal on example graph
- We have a graph whose vertices are A, B, C, D, E, F, G. Considering A as the starting point, the steps involved in the process are:
- Vertex A is expanded and stored in the queue.
- Vertices B, D, and G, as successors of A, are expanded and stored in the queue. Meanwhile, Vertex A is removed.
- Now B at the front end of the queue is removed along with storing its successor vertices E and F.
- Vertex D at the front end of the queue is removed, and its connected node F has already been visited.
- Vertex G is removed from the queue, and it has successor E which has already been visited.
- Now E and F are removed from the queue, and its successor vertex C is traversed and stored in the queue.
- At last C is also removed and the queue is now empty which means we are done.
- The generated Output is – A, B, D, G, E, F, C.
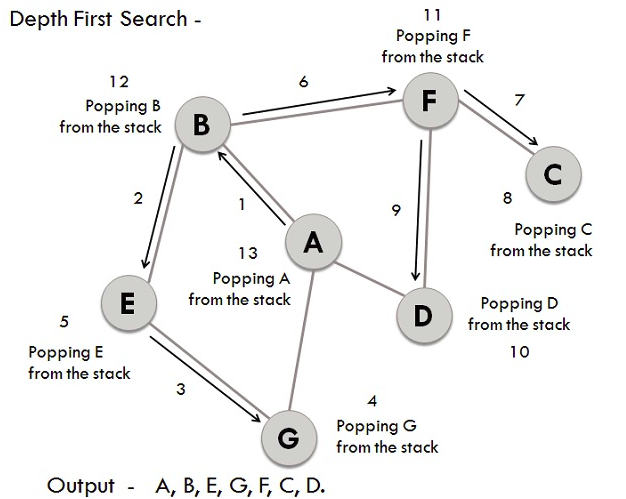
DFS traversal on example graph
Similar to BFS, let's take the same graph for performing DFS operations. The steps involved in the process are:
- Considering A as the starting vertex which is explored and stored in the stack.
- B, the successor vertex of A, is stored in the stack.
- Vertex B has two successors E and F, among them alphabetically E is explored first and stored in the stack.
- The successor of vertex E, i.e., G is stored in the stack.
- Vertex G has two connected vertices, and both are already visited, so G is popped out from the stack.
- Similarly, E is also removed.
- Now vertex B is at the top of the stack, its other successor(vertex) F is explored and stored in the stack.
- Vertex F has two successors C and D, between which C is traversed first and stored in the stack.
- Vertex C has only one predecessor which has already been visited, so it is removed from the stack.
- Now vertex D, which is connected to F is visited and stored in the stack.
- Since vertex D does not have any unvisited nodes, D is therefore removed.
- Similarly, F, B and A are also popped from the stack.
- The generated output is – A, B, E, G, F, C, D.