Language acceptance by Deterministic Finite Automata (DFAs)
Introduction
Consider the following example of a very rudimentary vending machine which only takes in 1 and 2 rupee coins as inputs, and all items are identical are priced at 5 rupees each. The vending machine pushes all the coins out if the input coins add up to 6 rupees without first adding up to 5 rupees, or any coin that is input after reaching 5 rupees.
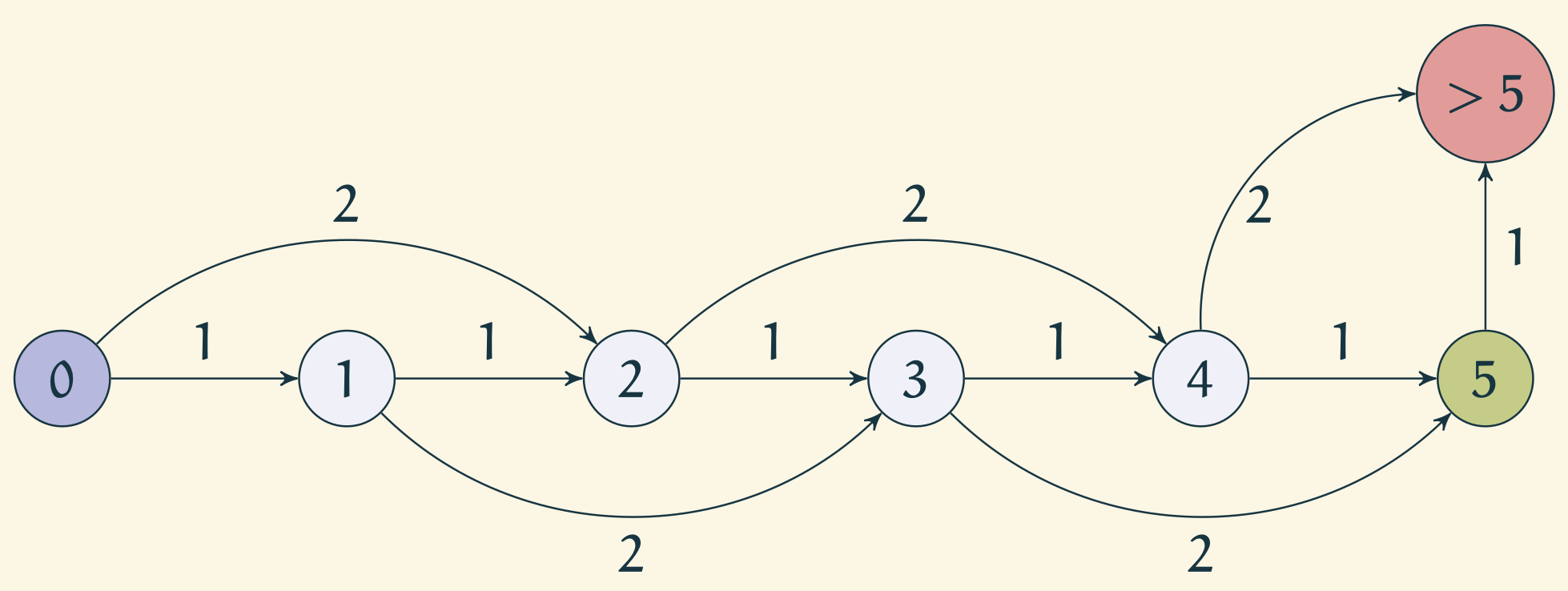
Observe that the machine can be in states 1, 2, 3, 4, 5, and >5 depending on what the sum of coins input so far is. For the machine, the sequence of coins input so far do not matter.
Abstracting out the machine
Note that the following properties held for the above machine.
- Finite number of states: ${0,1,2, \ldots, 5, >5}$
- Well defined input: ${1,2}^*$
- Predetermined transition logic
- Start state: ${0}$
- Actionable states: ${5, >5}$
- No memory of previous states
This is in fact an example of what we call a deterministic finite state machines or finite state automaton. In short, we refer to them as DFAs.
Formal definition
A Deterministic Finite State Machine/Automaton (DFA) is a $5$-tuple $(Q, \Sigma, \delta, q_0, F)$ where
- $Q$ is a finite set called states,
- $\Sigma$ is a finite set called alphabet,
- $\delta: Q\times \Sigma \rightarrow Q$ is the transition function,
- $q_0$ is the start state, and
- $F\subseteq Q$ is the set of accept states.
Afore mentioned rudimentary vending machine can be formalized as follows.
- $Q = {q_1, q_2, q_3, q_4, q_5, q_{>}}$
- $\Sigma = {1,2}$
- $\delta$ is given by
| 1 | 2 | |
|---|---|---|
| $q_0$ | $q_1$ | $q_2$ |
| $q_1$ | $q_2$ | $q_3$ |
| $q_2$ | $q_3$ | $q_4$ |
| $q_3$ | $q_4$ | $q_5$ |
| $q_4$ | $q_5$ | $q_{>}$ |
| $q_5$ | $q_{>}$ | $q_{>}$ |
| $q_{>}$ | $q_{>}$ | $q_{>}$ |
- $q_0$ is the start state
- $F = {q_5}$
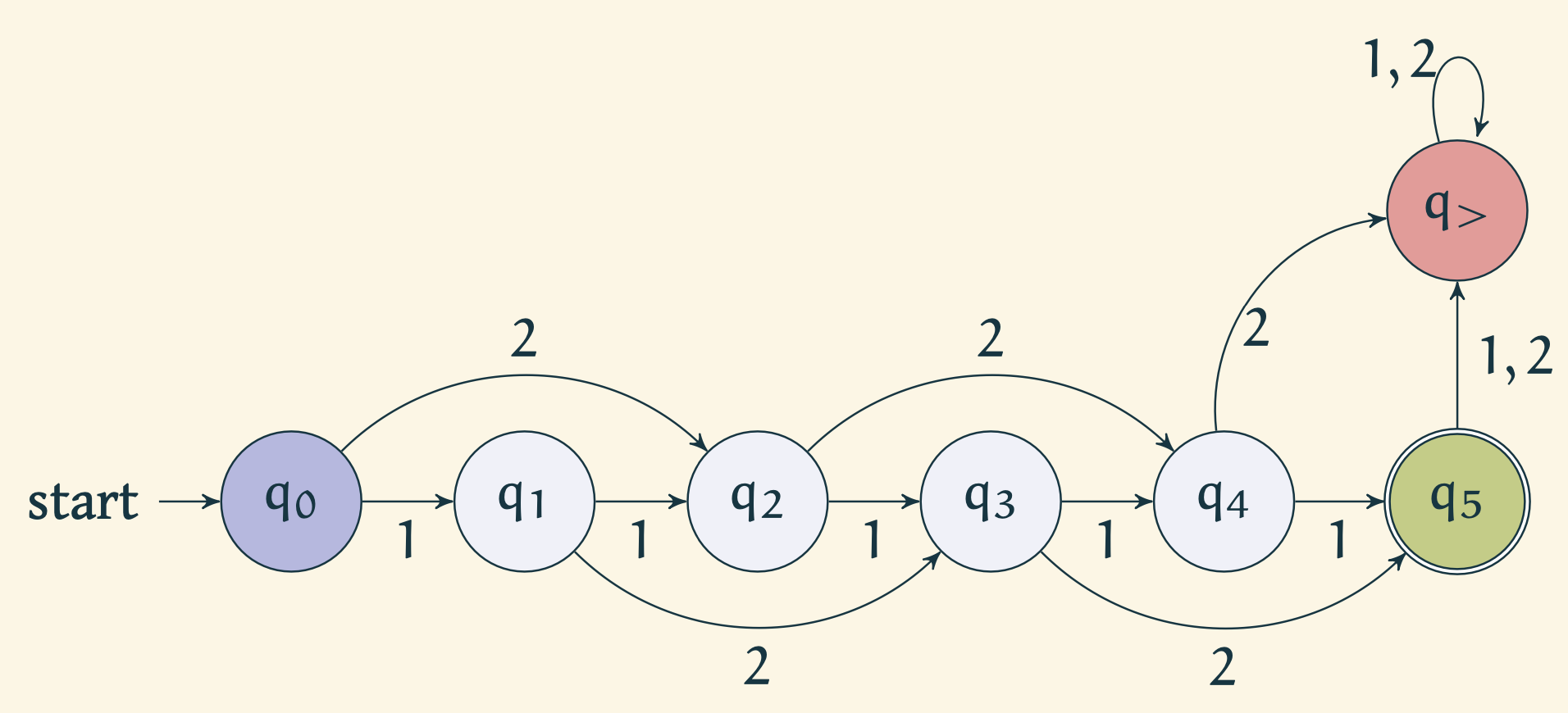
Run of a Finite State Automaton
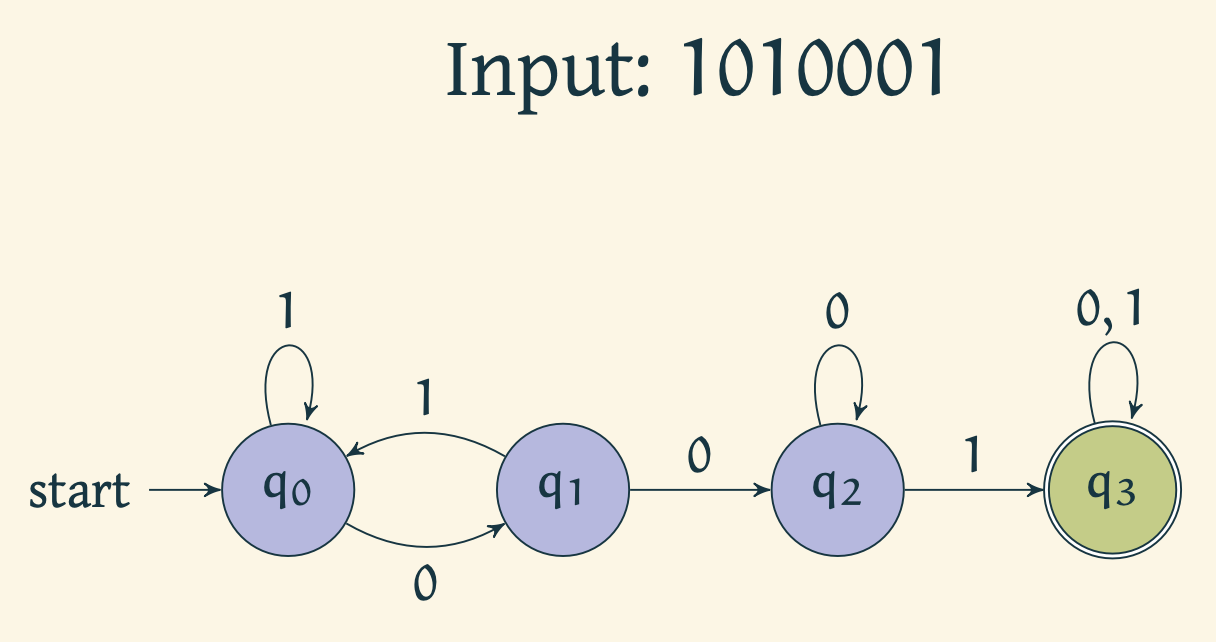
Given any string in $\Sigma^*$, we can simulate the finite state automaton using the predetermined transition function by reading the string bit by bit. Note that the start state is $q_0$, and the accept state is $q_3$.
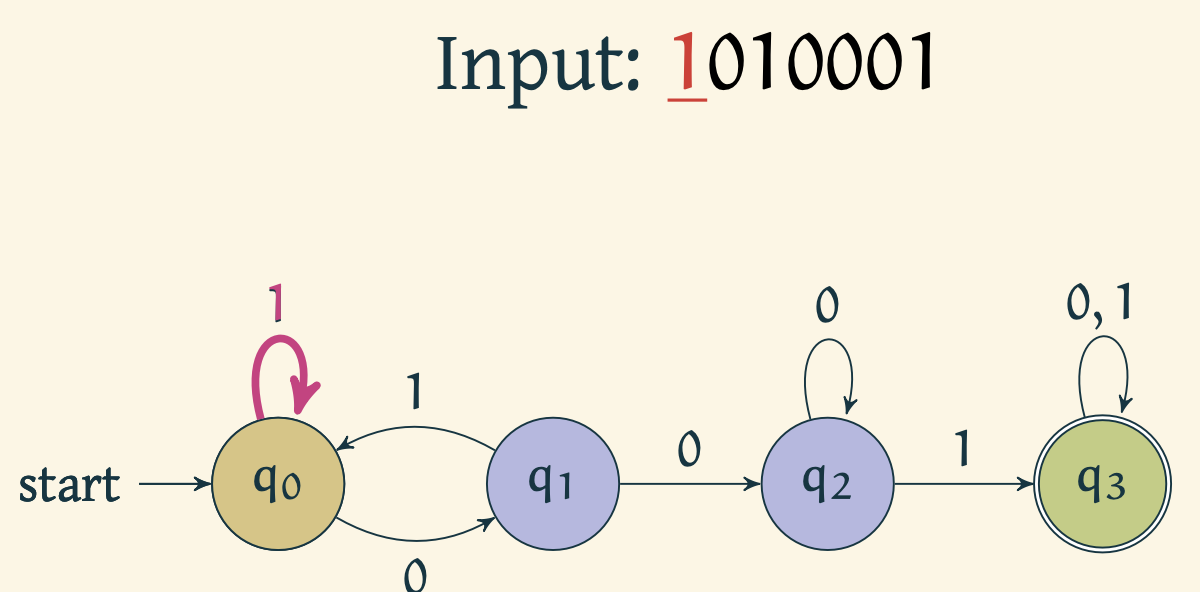
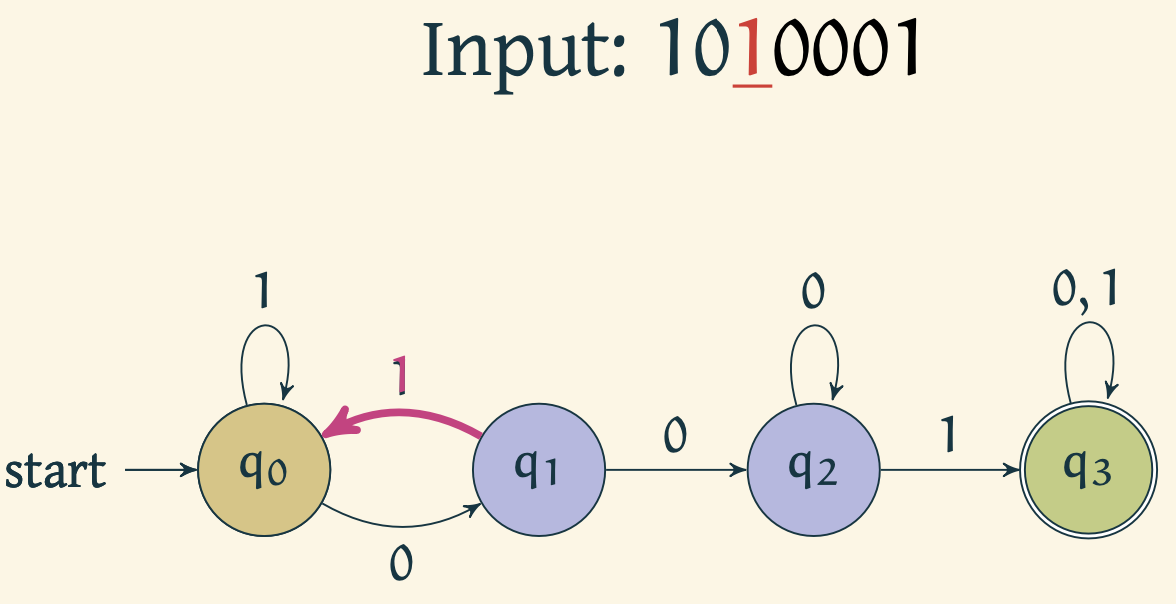
Automaton reads 1 and stays in $q_0$.
Automaton reads 0 and moves to $q_1$
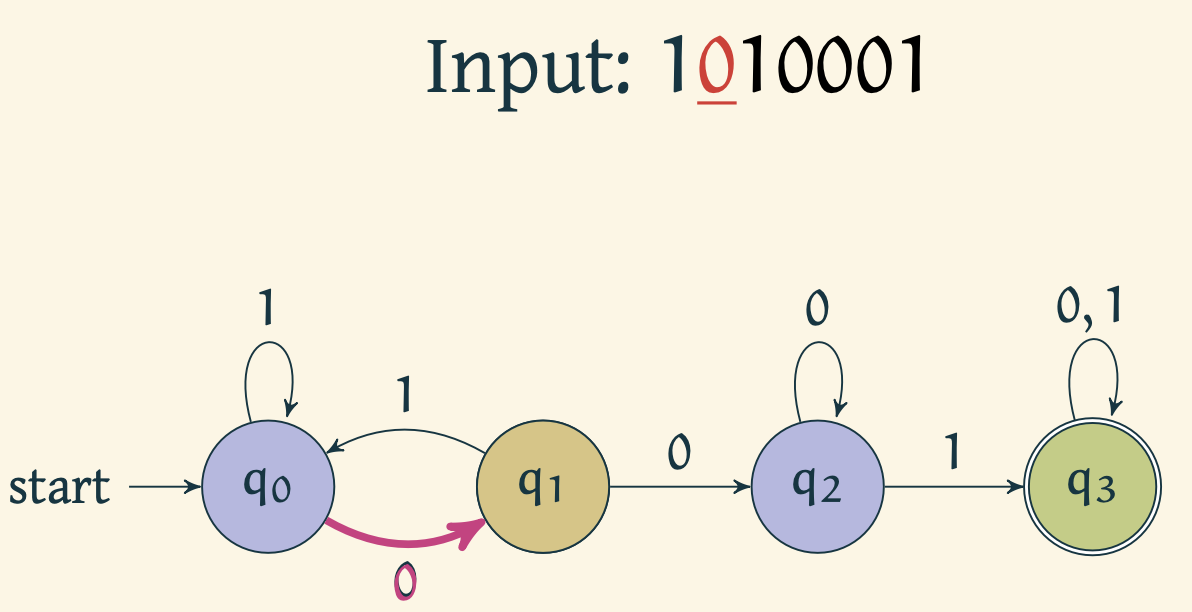
Automaton reads 1 and moves to $q_0$
Automaton reads 0 and moves to $q_1$
Automaton reads 0 and moves to $q_2$
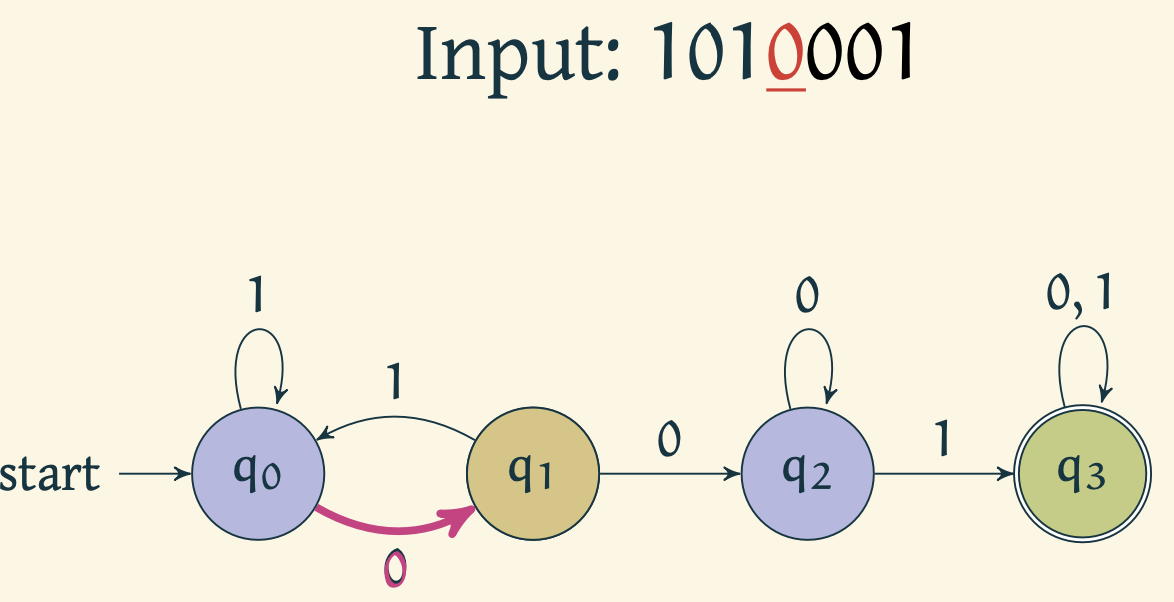
Automaton reads 0 and stays in $q_2$
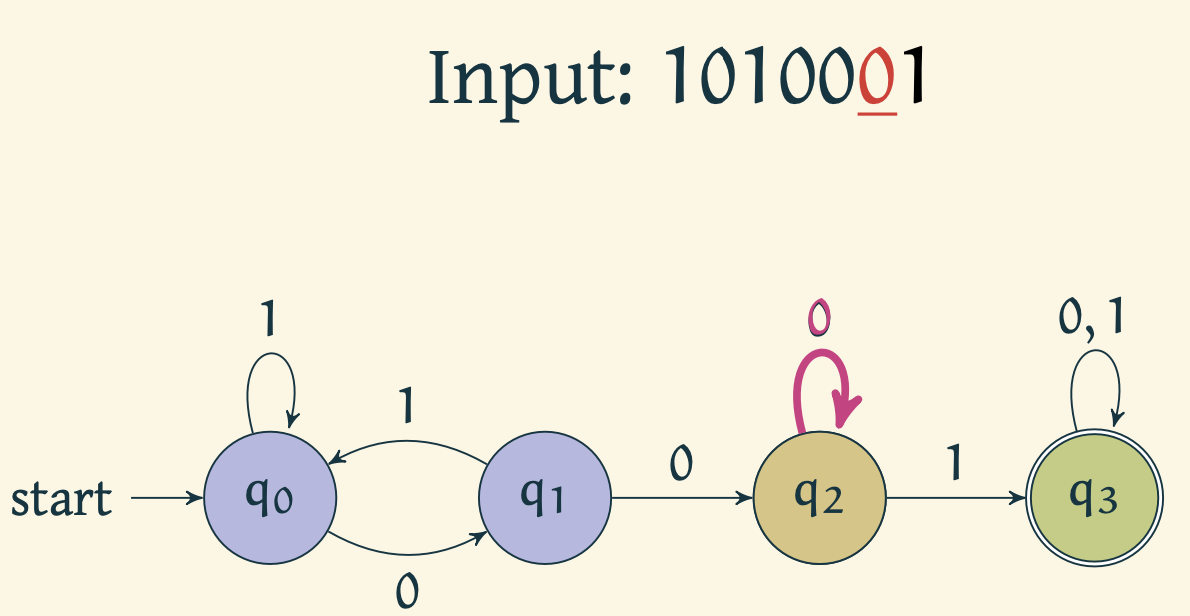
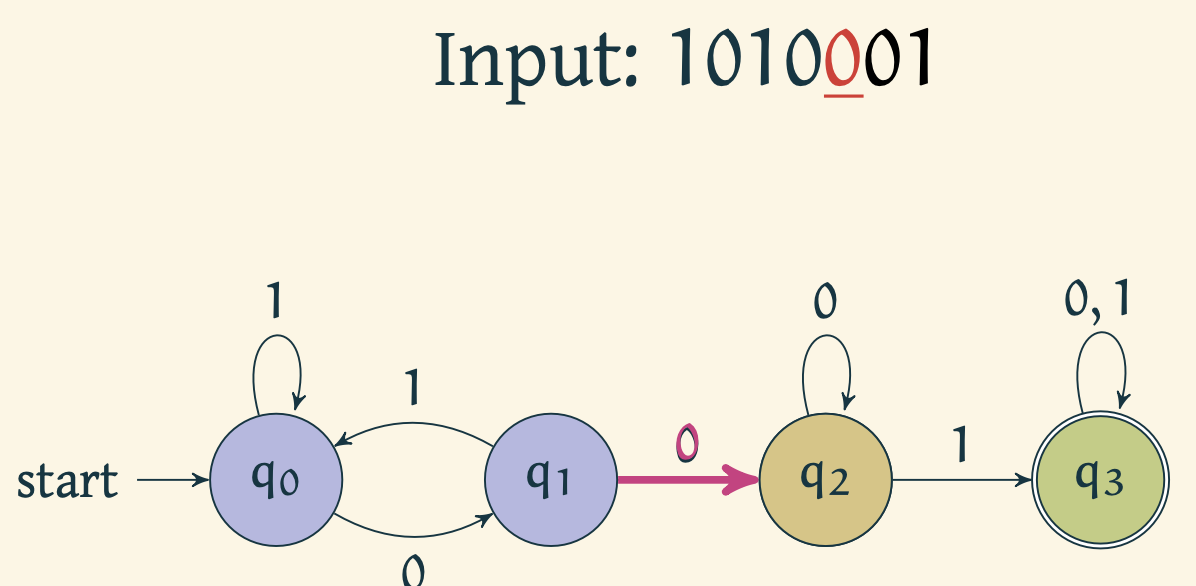
Automaton reads 1 and moves to $q_3$
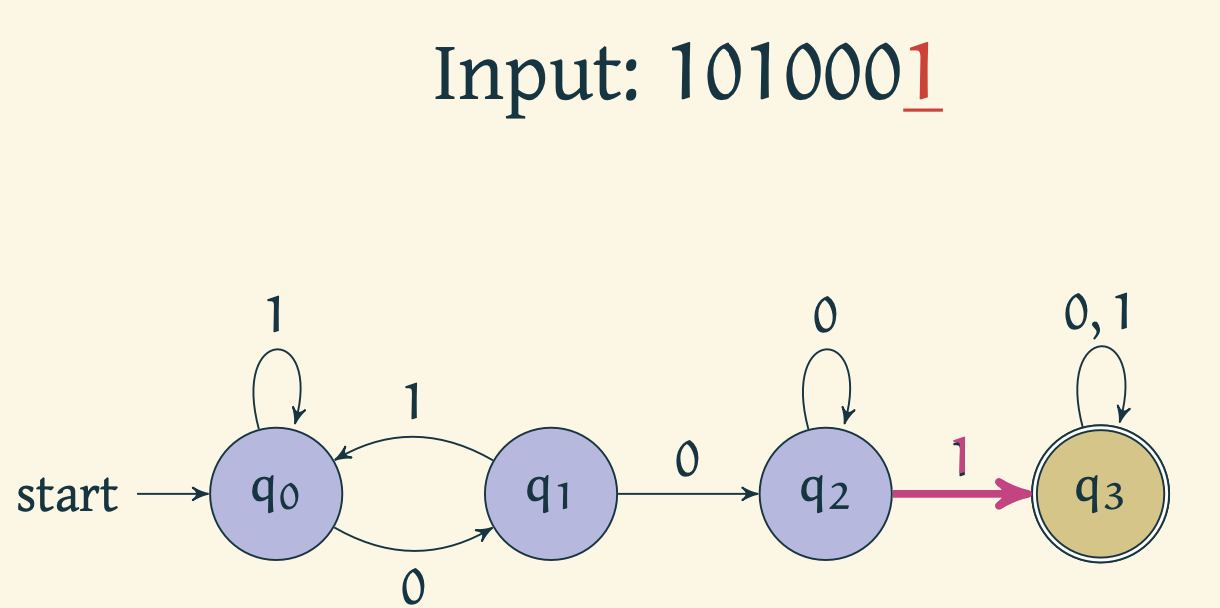
Automaton accepts the string upon reaching $q_3$.
Language acceptance of a finite state automaton
A language is a set of strings over a given alphabet $\Sigma$.
Given a machine $M = (Q, \Sigma, \delta, q_0, F)$,
- A string $x$ is accepted by machine $M$ if a run of machine $M$ on $x$ ends in an accepting state.
- Language of $M$, $L(M) = {w\in\Sigma^{*}\mid \text{$w$ is accepted by $M$}}$.
- For a set $A$ if $L(M) = A$, then $M$ recognizes $A$.
The above definition does not use the word deterministic, and as we shall see in the next experiment, this also holds for non-deterministic finite state automata.
Things to ponder on:
- Given a finite state automaton $M$, can it happen that it accepts no strings?
- Given a set of strings over an alphabet $\Sigma$, is there a DFA that accepts it?
Example 2
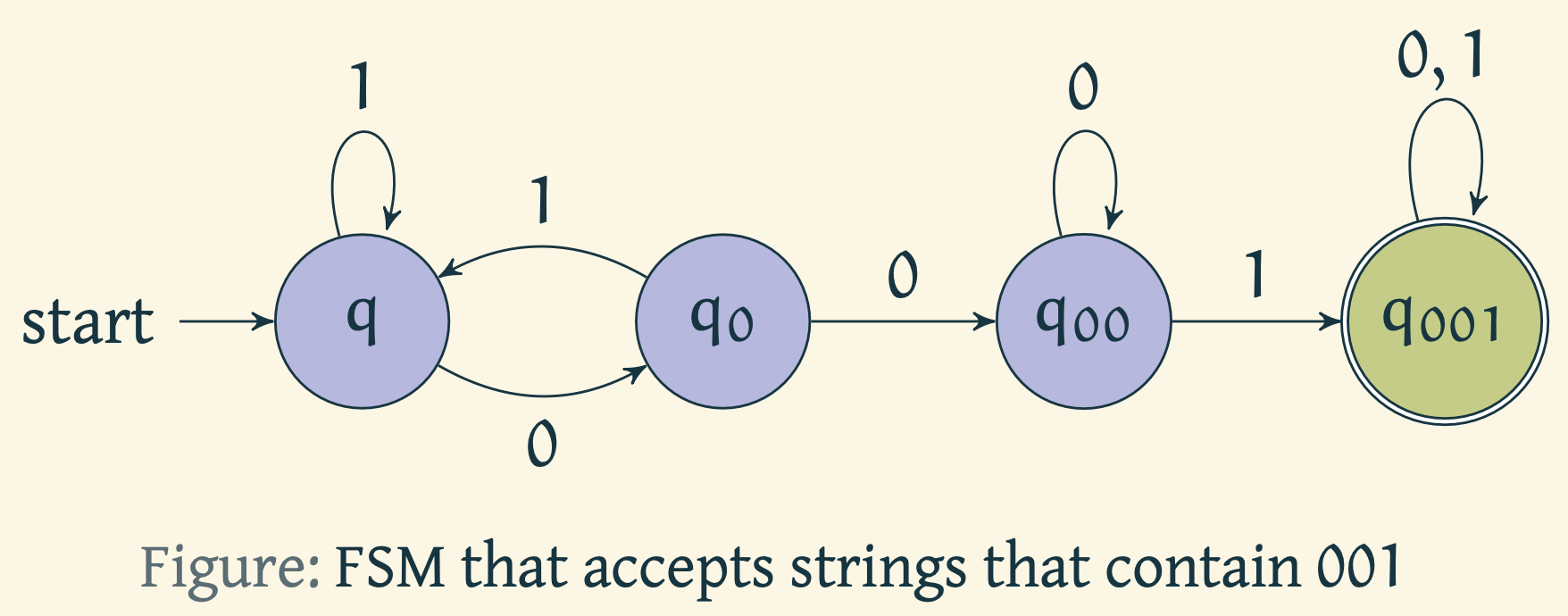
The above automaton recognizes strings that contain 001.