Introduction

CFGs can be ambiguous - which implies that multiple parse trees can be generated from the same input. For a string generated from ambiguous grammars, there exist multiple left-most or right-most derivations.

Left Most Derivation:

Left-most derivation of a string is done by replacing the left-most non-terminal symbol according to the corresponding production rule.

Right Most Derivation:

The right-most derivation of a string is done by replacing the right-most non-terminal symbol according to the corresponding production rule

Ambiguity in Context Free Grammar

A context free grammar G is called an ambiguous grammar if it has more than one derivation tree for a given string w ∈ L(G). There is no general algorithm that decides whether an arbitrary CFG is ambiguous. In practice we check ambiguity by constructing parse trees for specific input strings and seeing whether more than one distinct parse tree exists for that string. It should be noted that even in an ambiguous grammar, some strings may still have only one parse tree.

Examples

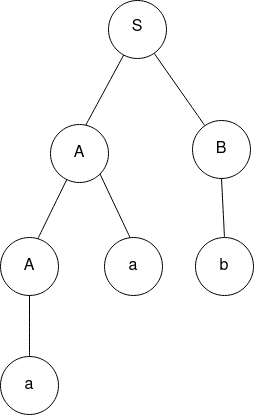
1. Consider the following grammar and construct the parse tree for the string $aab$

$$S → AB \\ A → Aa | a \\ B → b$$

For the string $aab$, there is only one parse tree possible, as shown below-

1. Check if the context-free grammar G is ambiguous

$$G = \{ S → SS, S → ab, S → ba, S → \epsilon \}$$

Let us consider the string $abab$. There are more than one left-most derivations for this string as given below-

$$S → SS → SSS → abSS → ababS → abab \\ S → SS → abS → abab$$

Hence, the grammar is ambiguous.

Equivalence of CFG and PDA — determinism and ambiguity

• CFG ↔ NPDA equivalence: For every context-free grammar there is an equivalent nondeterministic pushdown automaton (NPDA) that recognizes the same language, and conversely every PDA (in the nondeterministic sense) can be converted into an equivalent CFG. Together these constructions establish that the class of context-free languages (CFLs) equals the class of languages recognized by NPDAs.

• Deterministic PDAs (DPDA) vs NPDAs: A deterministic pushdown automaton (DPDA) recognizes a smaller class called deterministic context-free languages (DCFLs). DCFLs form a strict subset of CFLs — not every CFL can be accepted by a DPDA.

• Ambiguity (grammar) vs determinism (automaton): Ambiguity is a property of a grammar: an ambiguous grammar yields multiple parse trees for the same string. A language may be generated by both ambiguous and unambiguous grammars; some languages are inherently ambiguous (no unambiguous grammar exists). Determinism concerns the machine model: if a language is recognized by a DPDA, then it admits unambiguous parsing (i.e., an unambiguous grammar exists for it). However, the converse is not true: an unambiguous language need not be deterministic (it may require nondeterminism for recognition by a PDA).

• Practical consequence: Constructions showing CFG↔PDA equivalence use nondeterministic PDAs. Deterministic parsing techniques (LL, LR families) correspond to restricted grammar classes that avoid ambiguity and permit efficient deterministic parsing; these correspond to languages that a DPDA can handle.

• Example: The language of well-balanced parentheses is deterministic and has unambiguous grammars; some CFLs (and some grammars for otherwise simple languages) remain ambiguous unless restructured.

Questions and Answers

1. What is left-most derivation in a context-free grammar? A: Derivation where the left-most non-terminal is replaced at each step.
2. What is ambiguity in CFGs? A: A grammar is considered ambiguous when the CFG generates a string with more than one parse tree.
3. Why is it important to remove/resolve ambiguity in CFGs? A: Removing ambiguity ensures unique interpretation and avoids confusion and errors in parsing.
4. What is the importance of precedence and associativity? A: Precedence ans associativity define the order and grouping rules for expressions, which can be used to resolve ambiguity.
5. How does left-factoring help in resolving ambiguity? A: Left factoring combines common prefixes in the production rules, which can further eliminate ambiguity.

Practical Applications

A few practical examples highlighting the importance of resolving ambiguities in CFGs -

1. Compiler Design: Ambiguous grammars can cause confusion in compilation due to potentially forming multiple parse trees from the same source code. Removal of ambiguities ensure unique interpretation.
2. Programming Languages: Removing ambiguities will ensure that each statement/expression in the language has a unique and well-defined meaning.
3. Expression Evaluation: Ambiguities in precedence can lead to different interpretations of arithmetic expressions. By specifying proper precedence and associativity rules, consistent evaluation of expressions can be ensured.